Arrival Control in Quasi-Reversible Queueing Systems: Optimization and Reinforcement Learning

In this paper, we introduce a versatile scheme for optimizing the arrival rates of quasi-reversible queueing systems. We first propose an alternative definition of quasi-reversibility that encompasses reversibility and highlights the importance of the definition of customer classes. In a second time, we introduce balanced arrival control policies, which generalize the notion of balanced arrival rates introduced in the context of Whittle networks, to the much broader class of quasi-reversible queueing systems. We prove that supplementing a quasi-reversible queueing system with a balanced arrival-control policy preserves the quasi-reversibility, and we specify the form of the stationary measures. We revisit two canonical examples of quasi-reversible queueing systems, Whittle networks and order-independent queues. Lastly, we focus on the problem of admission control and leverage our results in the frameworks of optimization and reinforcement learning.

Optimizing Asynchronous Federated Learning: A Delicate Trade-Off Between Model-Parameter Staleness and Update Frequency

Synchronous federated learning (FL) scales poorly with the number of clients due to the straggler effect. Algorithms like FedAsync and GeneralizedFedAsync address this limitation by enabling asynchronous communication between clients and the central server. In this work, we rely on stochastic modeling to better understand the impact of design choices in asynchronous FL algorithms, such as the concurrency level and routing probabilities, and we leverage this knowledge to optimize loss. We characterize in particular a fundamental trade-off for optimizing asynchronous FL: minimizing gradient estimation errors by avoiding model parameter staleness, while also speeding up the system by increasing the throughput of model updates. Our two main contributions can be summarized as follows. First, we prove a discrete variant of Little's law to derive a closed-form expression for relative delay, a metric that quantifies staleness. This allows us to efficiently minimize the average loss per model update, which has been the gold standard in literature to date. Second, we observe that naively optimizing this metric leads us to slow down the system drastically by overemphazing staleness at the detriment of throughput. This motivates us to introduce an alternative metric that also takes system speed into account, for which we derive a tractable upper-bound that can be minimized numerically. Extensive numerical results show that these optimizations enhance accuracy by 10% to 30%.

Score-Aware Policy-Gradient Methods and Performance Guarantees using Local Lyapunov Conditions: Applications to Product-Form Stochastic Networks and Queueing Systems

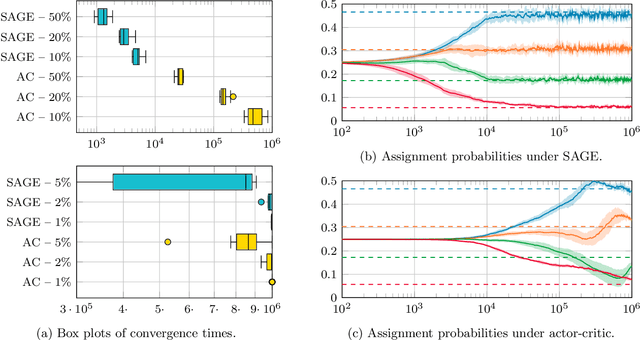
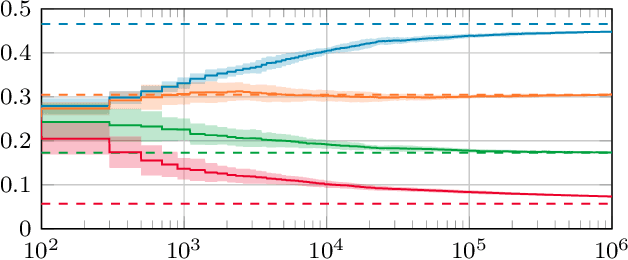
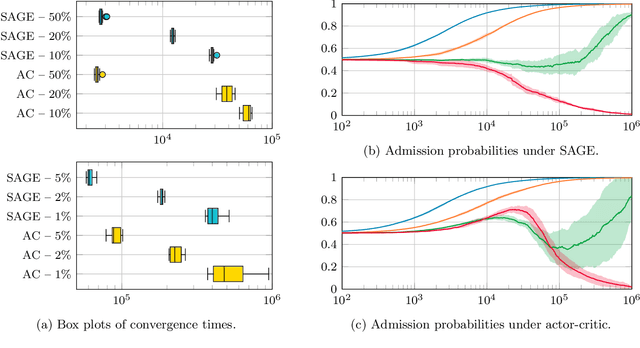
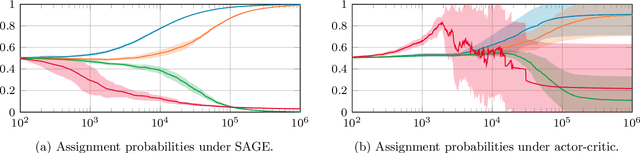
Stochastic networks and queueing systems often lead to Markov decision processes (MDPs) with large state and action spaces as well as nonconvex objective functions, which hinders the convergence of many reinforcement learning (RL) algorithms. Policy-gradient methods perform well on MDPs with large state and action spaces, but they sometimes experience slow convergence due to the high variance of the gradient estimator. In this paper, we show that some of these difficulties can be circumvented by exploiting the structure of the underlying MDP. We first introduce a new family of gradient estimators called score-aware gradient estimators (SAGEs). When the stationary distribution of the MDP belongs to an exponential family parametrized by the policy parameters, SAGEs allow us to estimate the policy gradient without relying on value-function estimation, contrary to classical policy-gradient methods like actor-critic. To demonstrate their applicability, we examine two common control problems arising in stochastic networks and queueing systems whose stationary distributions have a product-form, a special case of exponential families. As a second contribution, we show that, under appropriate assumptions, the policy under a SAGE-based policy-gradient method has a large probability of converging to an optimal policy, provided that it starts sufficiently close to it, even with a nonconvex objective function and multiple maximizers. Our key assumptions are that, locally around a maximizer, a nondegeneracy property of the Hessian of the objective function holds and a Lyapunov function exists. Finally, we conduct a numerical comparison between a SAGE-based policy-gradient method and an actor-critic algorithm. The results demonstrate that the SAGE-based method finds close-to-optimal policies more rapidly, highlighting its superior performance over the traditional actor-critic method.