Jan Melchior
A Hippocampus Model for Online One-Shot Storage of Pattern Sequences
May 30, 2019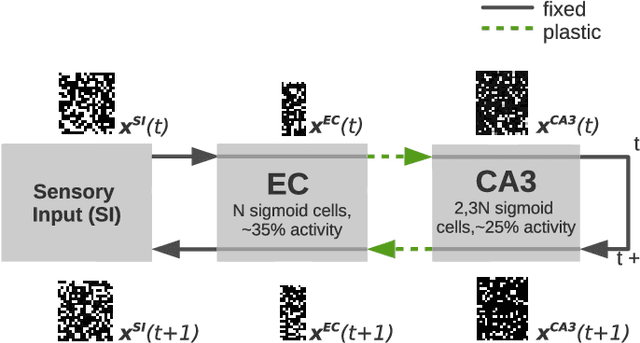
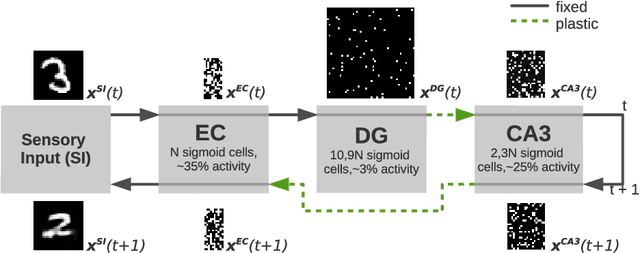
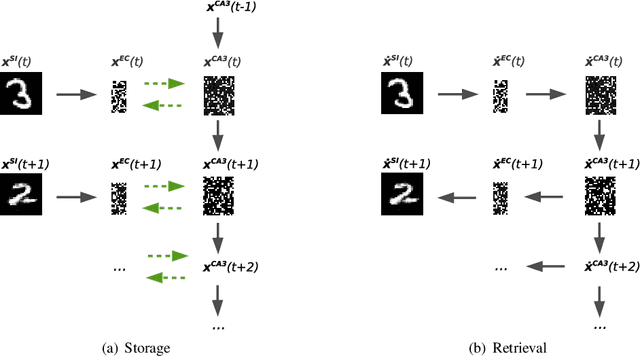
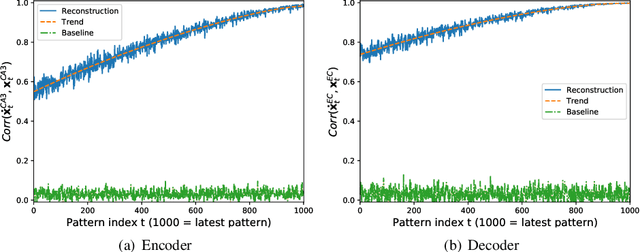
Abstract:We present a computational model based on the CRISP theory (Content Representation, Intrinsic Sequences, and Pattern completion) of the hippocampus that allows to continuously store pattern sequences online in a one-shot fashion. Rather than storing a sequence in CA3, CA3 provides a pre-trained sequence that is hetero-associated with the input sequence, which allows the system to perform one-shot learning. Plasticity on a short time scale therefore only happens in the incoming and outgoing connections of CA3. Stored sequences can later be recalled from a single cue pattern. We identify the pattern separation performed by subregion DG to be necessary for storing sequences that contain correlated patterns. A design principle of the model is that we use a single learning rule named Hebbiand-escent to train all parts of the system. Hebbian-descent has an inherent forgetting mechanism that allows the system to continuously memorize new patterns while forgetting early stored ones. The model shows a plausible behavior when noisy and new patterns are presented and has a rather high capacity of about 40% in terms of the number of neurons in CA3. One notable property of our model is that it is capable of `boot-strapping' (improving) itself without external input in a process we refer to as `dreaming'. Besides artificially generated input sequences we also show that the model works with sequences of encoded handwritten digits or natural images. To our knowledge this is the first model of the hippocampus that allows to store correlated pattern sequences online in a one-shot fashion without a consolidation process, which can instantaneously be recalled later.
Hebbian-Descent
May 25, 2019
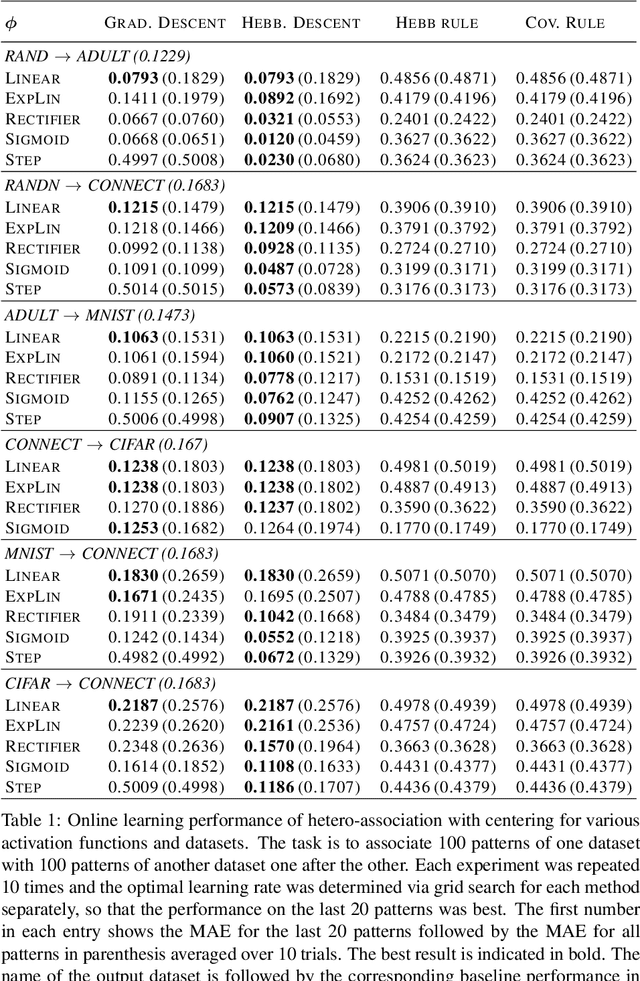


Abstract:In this work we propose Hebbian-descent as a biologically plausible learning rule for hetero-associative as well as auto-associative learning in single layer artificial neural networks. It can be used as a replacement for gradient descent as well as Hebbian learning, in particular in online learning, as it inherits their advantages while not suffering from their disadvantages. We discuss the drawbacks of Hebbian learning as having problems with correlated input data and not profiting from seeing training patterns several times. For gradient descent we identify the derivative of the activation function as problematic especially in online learning. Hebbian-descent addresses these problems by getting rid of the activation function's derivative and by centering, i.e. keeping the neural activities mean free, leading to a biologically plausible update rule that is provably convergent, does not suffer from the vanishing error term problem, can deal with correlated data, profits from seeing patterns several times, and enables successful online learning when centering is used. We discuss its relationship to Hebbian learning, contrastive learning, and gradient decent and show that in case of a strictly positive derivative of the activation function Hebbian-descent leads to the same update rule as gradient descent but for a different loss function. In this case Hebbian-descent inherits the convergence properties of gradient descent, but we also show empirically that it converges when the derivative of the activation function is only non-negative, such as for the step function for example. Furthermore, in case of the mean squared error loss Hebbian-descent can be understood as the difference between two Hebb-learning steps, which in case of an invertible and integrable activation function actually optimizes a generalized linear model. ...
How to Center Binary Deep Boltzmann Machines
Jul 16, 2015



Abstract:This work analyzes centered binary Restricted Boltzmann Machines (RBMs) and binary Deep Boltzmann Machines (DBMs), where centering is done by subtracting offset values from visible and hidden variables. We show analytically that (i) centering results in a different but equivalent parameterization for artificial neural networks in general, (ii) the expected performance of centered binary RBMs/DBMs is invariant under simultaneous flip of data and offsets, for any offset value in the range of zero to one, (iii) centering can be reformulated as a different update rule for normal binary RBMs/DBMs, and (iv) using the enhanced gradient is equivalent to setting the offset values to the average over model and data mean. Furthermore, numerical simulations suggest that (i) optimal generative performance is achieved by subtracting mean values from visible as well as hidden variables, (ii) centered RBMs/DBMs reach significantly higher log-likelihood values than normal binary RBMs/DBMs, (iii) centering variants whose offsets depend on the model mean, like the enhanced gradient, suffer from severe divergence problems, (iv) learning is stabilized if an exponentially moving average over the batch means is used for the offset values instead of the current batch mean, which also prevents the enhanced gradient from diverging, (v) centered RBMs/DBMs reach higher LL values than normal RBMs/DBMs while having a smaller norm of the weight matrix, (vi) centering leads to an update direction that is closer to the natural gradient and that the natural gradient is extremly efficient for training RBMs, (vii) centering dispense the need for greedy layer-wise pre-training of DBMs, (viii) furthermore we show that pre-training often even worsen the results independently whether centering is used or not, and (ix) centering is also beneficial for auto encoders.
* Author list in meta data corrected - 57 pages, 17 figures, 13 tables
Gaussian-binary Restricted Boltzmann Machines on Modeling Natural Image Statistics
Jan 23, 2014
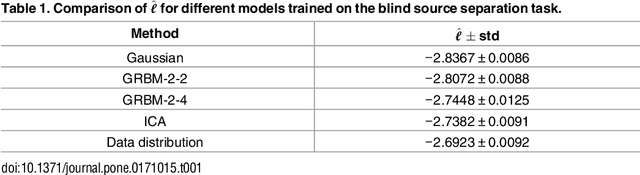
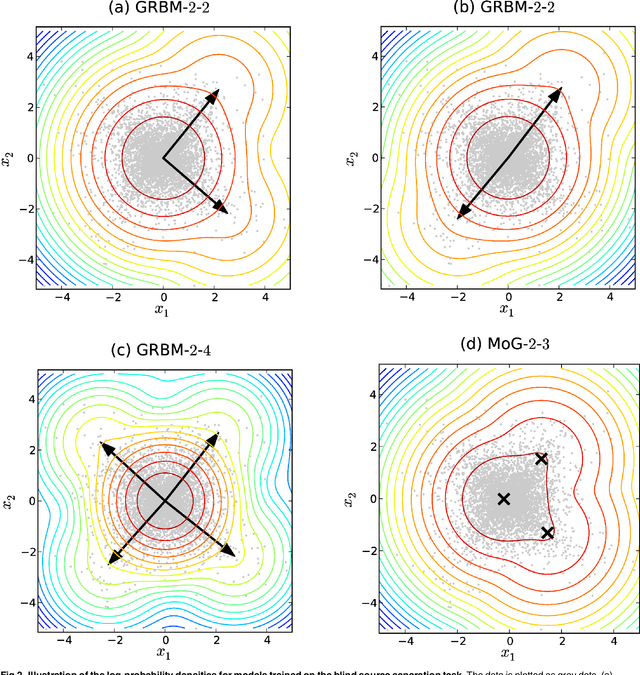

Abstract:We present a theoretical analysis of Gaussian-binary restricted Boltzmann machines (GRBMs) from the perspective of density models. The key aspect of this analysis is to show that GRBMs can be formulated as a constrained mixture of Gaussians, which gives a much better insight into the model's capabilities and limitations. We show that GRBMs are capable of learning meaningful features both in a two-dimensional blind source separation task and in modeling natural images. Further, we show that reported difficulties in training GRBMs are due to the failure of the training algorithm rather than the model itself. Based on our analysis we are able to propose several training recipes, which allowed successful and fast training in our experiments. Finally, we discuss the relationship of GRBMs to several modifications that have been proposed to improve the model.
* Current version is only an early manuscript and is subject to further change
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge