Efficient Multi-Object Tracking on Edge Devices via Reconstruction-Based Channel Pruning

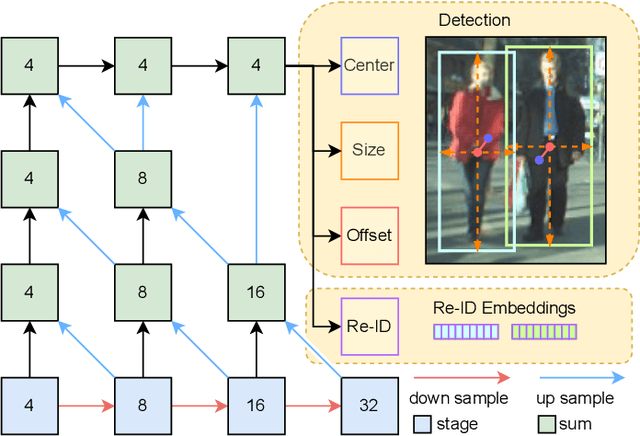
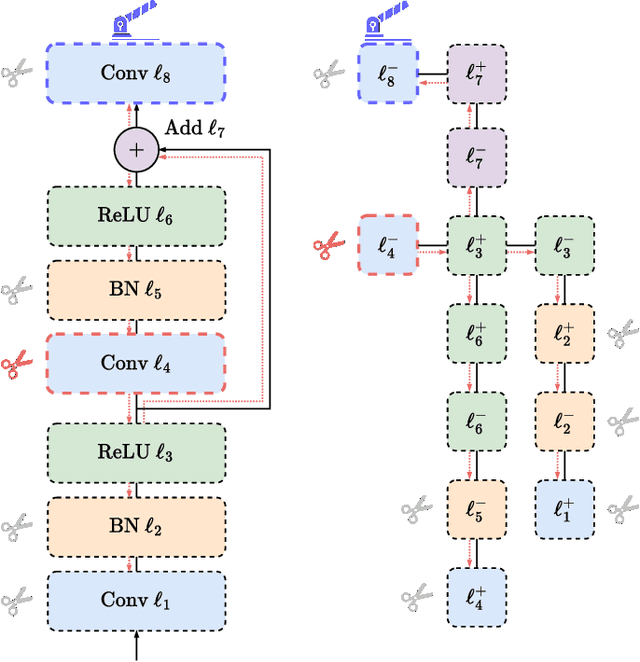
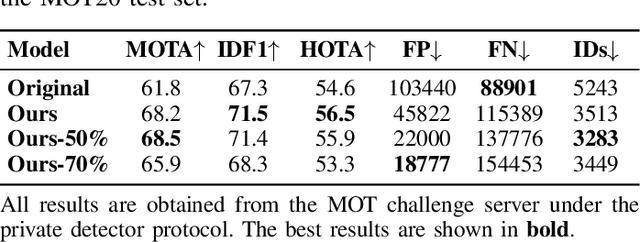
The advancement of multi-object tracking (MOT) technologies presents the dual challenge of maintaining high performance while addressing critical security and privacy concerns. In applications such as pedestrian tracking, where sensitive personal data is involved, the potential for privacy violations and data misuse becomes a significant issue if data is transmitted to external servers. To mitigate these risks, processing data directly on an edge device, such as a smart camera, has emerged as a viable solution. Edge computing ensures that sensitive information remains local, thereby aligning with stringent privacy principles and significantly reducing network latency. However, the implementation of MOT on edge devices is not without its challenges. Edge devices typically possess limited computational resources, necessitating the development of highly optimized algorithms capable of delivering real-time performance under these constraints. The disparity between the computational requirements of state-of-the-art MOT algorithms and the capabilities of edge devices emphasizes a significant obstacle. To address these challenges, we propose a neural network pruning method specifically tailored to compress complex networks, such as those used in modern MOT systems. This approach optimizes MOT performance by ensuring high accuracy and efficiency within the constraints of limited edge devices, such as NVIDIA's Jetson Orin Nano. By applying our pruning method, we achieve model size reductions of up to 70% while maintaining a high level of accuracy and further improving performance on the Jetson Orin Nano, demonstrating the effectiveness of our approach for edge computing applications.

Neural inverse procedural modeling of knitting yarns from images

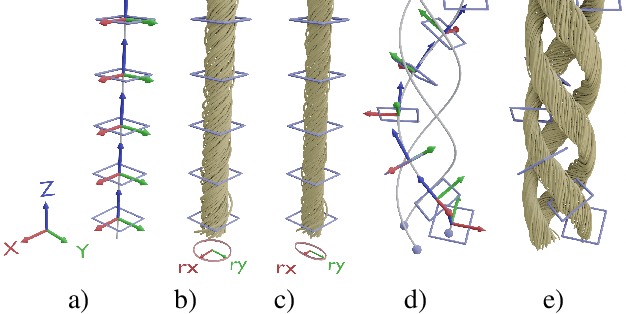
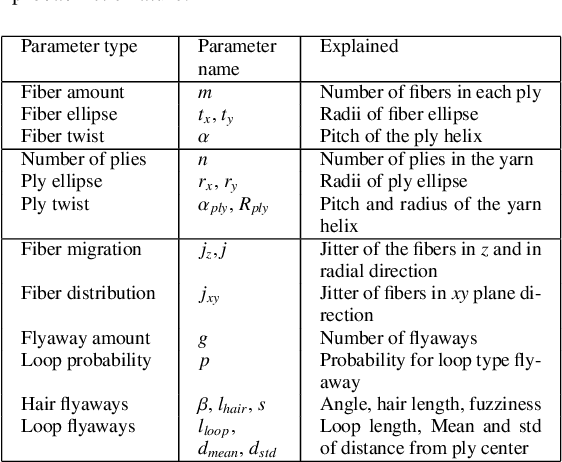
We investigate the capabilities of neural inverse procedural modeling to infer high-quality procedural yarn models with fiber-level details from single images of depicted yarn samples. While directly inferring all parameters of the underlying yarn model based on a single neural network may seem an intuitive choice, we show that the complexity of yarn structures in terms of twisting and migration characteristics of the involved fibers can be better encountered in terms of ensembles of networks that focus on individual characteristics. We analyze the effect of different loss functions including a parameter loss to penalize the deviation of inferred parameters to ground truth annotations, a reconstruction loss to enforce similar statistics of the image generated for the estimated parameters in comparison to training images as well as an additional regularization term to explicitly penalize deviations between latent codes of synthetic images and the average latent code of real images in the latent space of the encoder. We demonstrate that the combination of a carefully designed parametric, procedural yarn model with respective network ensembles as well as loss functions even allows robust parameter inference when solely trained on synthetic data. Since our approach relies on the availability of a yarn database with parameter annotations and we are not aware of such a respectively available dataset, we additionally provide, to the best of our knowledge, the first dataset of yarn images with annotations regarding the respective yarn parameters. For this purpose, we use a novel yarn generator that improves the realism of the produced results over previous approaches.

Orthogonal Wasserstein GANs

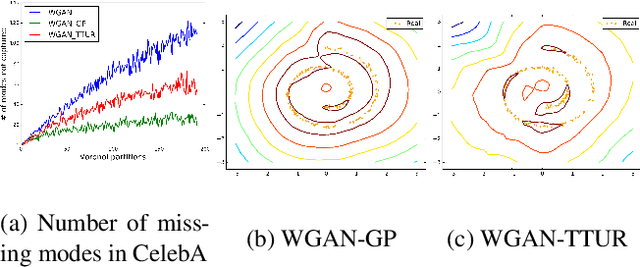
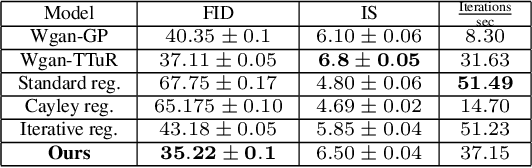
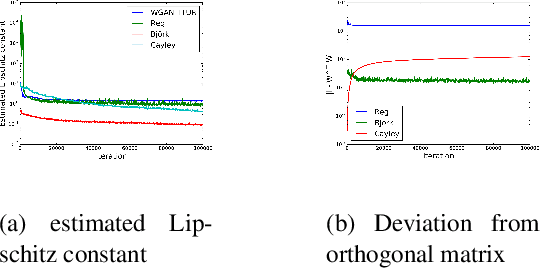
Wasserstein-GANs have been introduced to address the deficiencies of generative adversarial networks (GANs) regarding the problems of vanishing gradients and mode collapse during the training, leading to improved convergence behaviour and improved image quality. However, Wasserstein-GANs require the discriminator to be Lipschitz continuous. In current state-of-the-art Wasserstein-GANs this constraint is enforced via gradient norm regularization. In this paper, we demonstrate that this regularization does not encourage a broad distribution of spectral-values in the discriminator weights, hence resulting in less fidelity in the learned distribution. We therefore investigate the possibility of substituting this Lipschitz constraint with an orthogonality constraint on the weight matrices. We compare three different weight orthogonalization techniques with regards to their convergence properties, their ability to ensure the Lipschitz condition and the achieved quality of the learned distribution. In addition, we provide a comparison to Wasserstein-GANs trained with current state-of-the-art methods, where we demonstrate the potential of solely using orthogonality-based regularization. In this context, we propose an improved training procedure for Wasserstein-GANs which utilizes orthogonalization to further increase its generalization capability. Finally, we provide a novel metric to evaluate the generalization capabilities of the discriminators of different Wasserstein-GANs.