Approximate Equivariance SO(3) Needlet Convolution

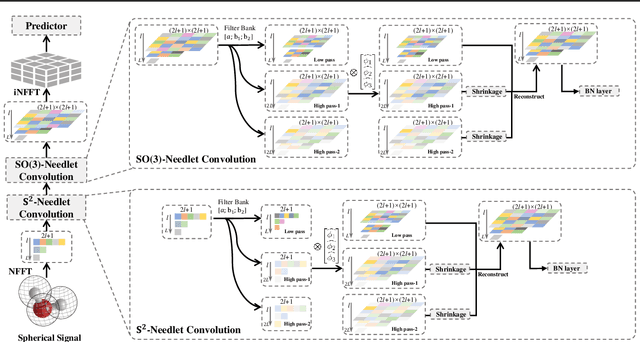
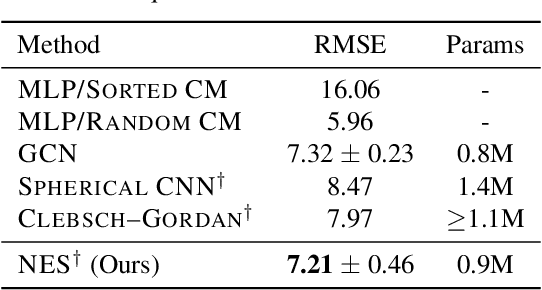
This paper develops a rotation-invariant needlet convolution for rotation group SO(3) to distill multiscale information of spherical signals. The spherical needlet transform is generalized from $\mathbb{S}^2$ onto the SO(3) group, which decomposes a spherical signal to approximate and detailed spectral coefficients by a set of tight framelet operators. The spherical signal during the decomposition and reconstruction achieves rotation invariance. Based on needlet transforms, we form a Needlet approximate Equivariance Spherical CNN (NES) with multiple SO(3) needlet convolutional layers. The network establishes a powerful tool to extract geometric-invariant features of spherical signals. The model allows sufficient network scalability with multi-resolution representation. A robust signal embedding is learned with wavelet shrinkage activation function, which filters out redundant high-pass representation while maintaining approximate rotation invariance. The NES achieves state-of-the-art performance for quantum chemistry regression and Cosmic Microwave Background (CMB) delensing reconstruction, which shows great potential for solving scientific challenges with high-resolution and multi-scale spherical signal representation.

CosmoVAE: Variational Autoencoder for CMB Image Inpainting

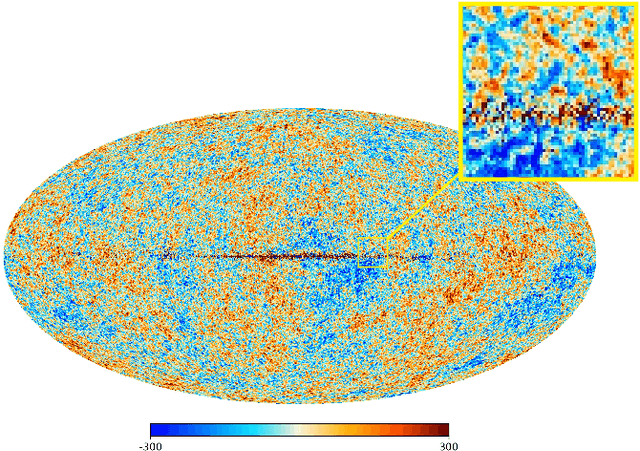
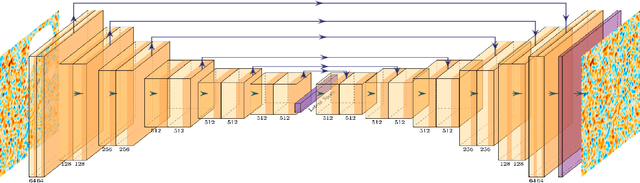
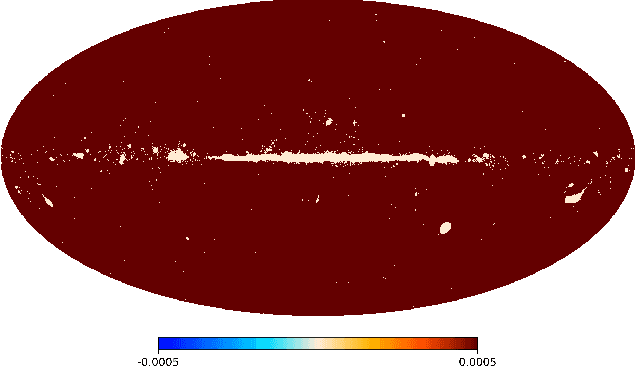
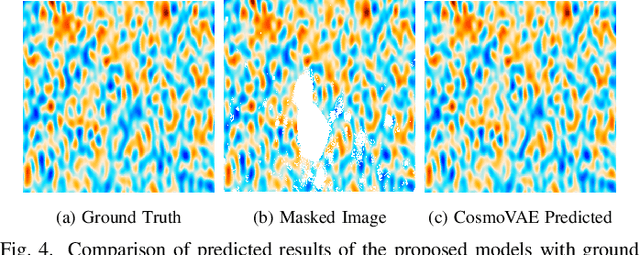
Cosmic microwave background radiation (CMB) is critical to the understanding of the early universe and precise estimation of cosmological constants. Due to the contamination of thermal dust noise in the galaxy, the CMB map that is an image on the two-dimensional sphere has missing observations, mainly concentrated on the equatorial region. The noise of the CMB map has a significant impact on the estimation precision for cosmological parameters. Inpainting the CMB map can effectively reduce the uncertainty of parametric estimation. In this paper, we propose a deep learning-based variational autoencoder --- CosmoVAE, to restoring the missing observations of the CMB map. The input and output of CosmoVAE are square images. To generate training, validation, and test data sets, we segment the full-sky CMB map into many small images by Cartesian projection. CosmoVAE assigns physical quantities to the parameters of the VAE network by using the angular power spectrum of the Gaussian random field as latent variables. CosmoVAE adopts a new loss function to improve the learning performance of the model, which consists of $\ell_1$ reconstruction loss, Kullback-Leibler divergence between the posterior distribution of encoder network and the prior distribution of latent variables, perceptual loss, and total-variation regularizer. The proposed model achieves state of the art performance for Planck \texttt{Commander} 2018 CMB map inpainting.