Bayesian System Identification based on Hierarchical Sparse Bayesian Learning and Gibbs Sampling with Application to Structural Damage Assessment

The focus in this paper is Bayesian system identification based on noisy incomplete modal data where we can impose spatially-sparse stiffness changes when updating a structural model. To this end, based on a similar hierarchical sparse Bayesian learning model from our previous work, we propose two Gibbs sampling algorithms. The algorithms differ in their strategies to deal with the posterior uncertainty of the equation-error precision parameter, but both sample from the conditional posterior probability density functions (PDFs) for the structural stiffness parameters and system modal parameters. The effective dimension for the Gibbs sampling is low because iterative sampling is done from only three conditional posterior PDFs that correspond to three parameter groups, along with sampling of the equation-error precision parameter from another conditional posterior PDF in one of the algorithms where it is not integrated out as a "nuisance" parameter. A nice feature from a computational perspective is that it is not necessary to solve a nonlinear eigenvalue problem of a structural model. The effectiveness and robustness of the proposed algorithms are illustrated by applying them to the IASE-ASCE Phase II simulated and experimental benchmark studies. The goal is to use incomplete modal data identified before and after possible damage to detect and assess spatially-sparse stiffness reductions induced by any damage. Our past and current focus on meeting challenges arising from Bayesian inference of structural stiffness serve to strengthen the capability of vibration-based structural system identification but our methods also have much broader applicability for inverse problems in science and technology where system matrices are to be inferred from noisy partial information about their eigenquantities.

Robust Bayesian compressive sensing with data loss recovery for structural health monitoring signals

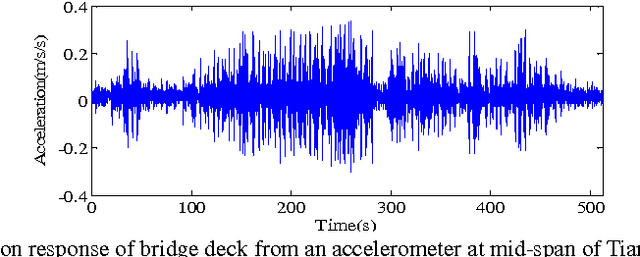
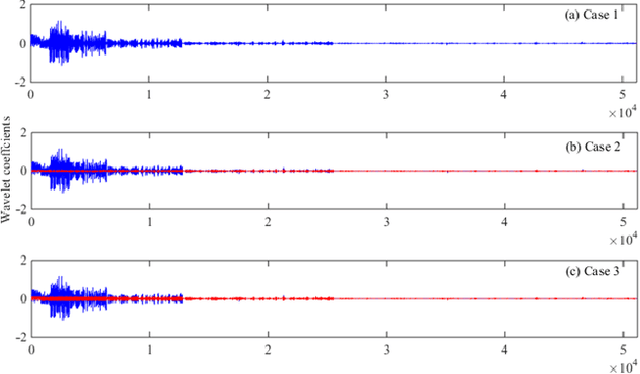
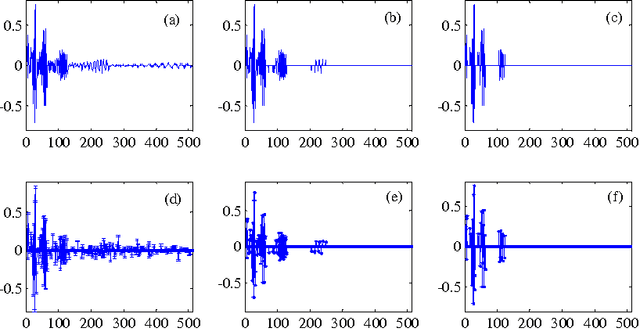
The application of compressive sensing (CS) to structural health monitoring is an emerging research topic. The basic idea in CS is to use a specially-designed wireless sensor to sample signals that are sparse in some basis (e.g. wavelet basis) directly in a compressed form, and then to reconstruct (decompress) these signals accurately using some inversion algorithm after transmission to a central processing unit. However, most signals in structural health monitoring are only approximately sparse, i.e. only a relatively small number of the signal coefficients in some basis are significant, but the other coefficients are usually not exactly zero. In this case, perfect reconstruction from compressed measurements is not expected. A new Bayesian CS algorithm is proposed in which robust treatment of the uncertain parameters is explored, including integration over the prediction-error precision parameter to remove it as a "nuisance" parameter. The performance of the new CS algorithm is investigated using compressed data from accelerometers installed on a space-frame structure and on a cable-stayed bridge. Compared with other state-of-the-art CS methods including our previously-published Bayesian method which uses MAP (maximum a posteriori) estimation of the prediction-error precision parameter, the new algorithm shows superior performance in reconstruction robustness and posterior uncertainty quantification. Furthermore, our method can be utilized for recovery of lost data during wireless transmission, regardless of the level of sparseness in the signal.

Hierarchical sparse Bayesian learning: theory and application for inferring structural damage from incomplete modal data

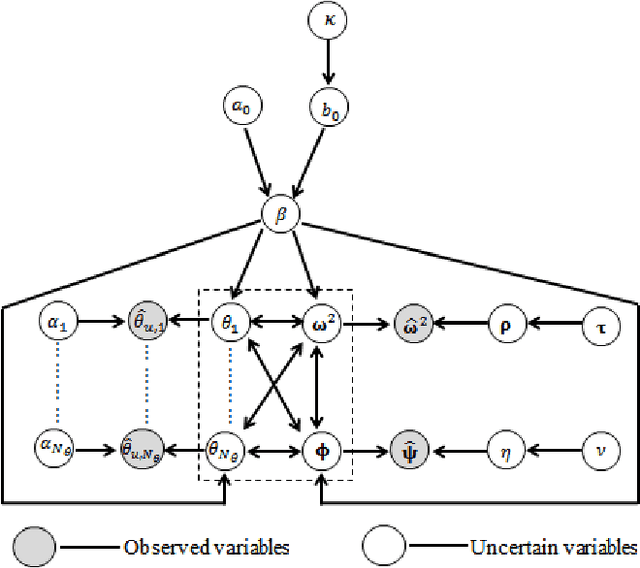
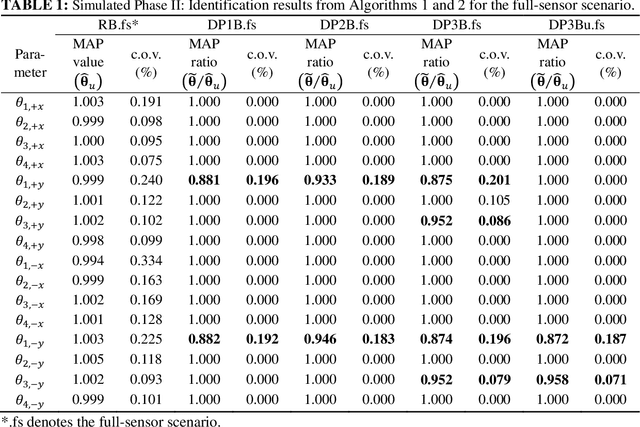
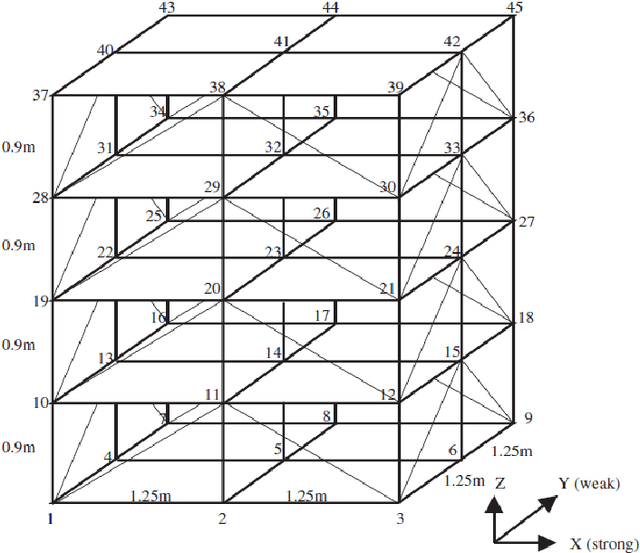
Structural damage due to excessive loading or environmental degradation typically occurs in localized areas in the absence of collapse. This prior information about the spatial sparseness of structural damage is exploited here by a hierarchical sparse Bayesian learning framework with the goal of reducing the source of ill-conditioning in the stiffness loss inversion problem for damage detection. Sparse Bayesian learning methodologies automatically prune away irrelevant or inactive features from a set of potential candidates, and so they are effective probabilistic tools for producing sparse explanatory subsets. We have previously proposed such an approach to establish the probability of localized stiffness reductions that serve as a proxy for damage by using noisy incomplete modal data from before and after possible damage. The core idea centers on a specific hierarchical Bayesian model that promotes spatial sparseness in the inferred stiffness reductions in a way that is consistent with the Bayesian Ockham razor. In this paper, we improve the theory of our previously proposed sparse Bayesian learning approach by eliminating an approximation and, more importantly, incorporating a constraint on stiffness increases. Our approach has many appealing features that are summarized at the end of the paper. We validate the approach by applying it to the Phase II simulated and experimental benchmark studies sponsored by the IASC-ASCE Task Group on Structural Health Monitoring. The results show that it can reliably detect, locate and assess damage by inferring substructure stiffness losses from the identified modal parameters. The occurrence of missed and false damage alerts is effectively suppressed.

Asymptotically Independent Markov Sampling: a new MCMC scheme for Bayesian Inference

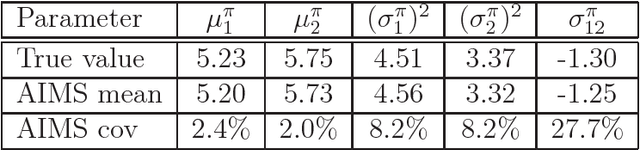
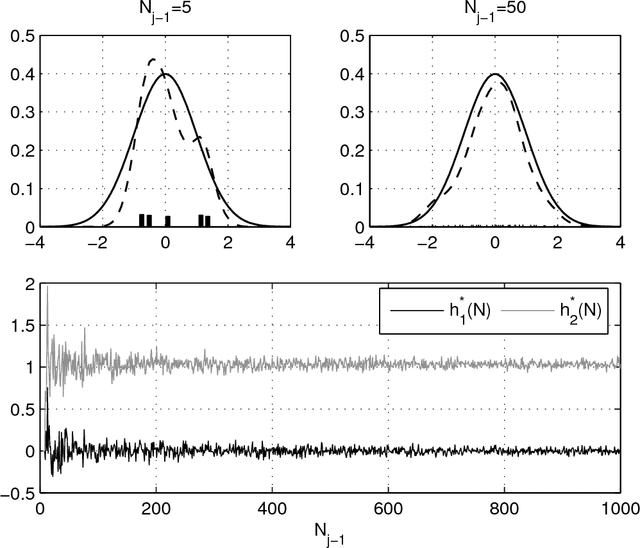
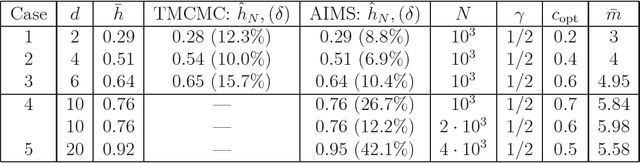
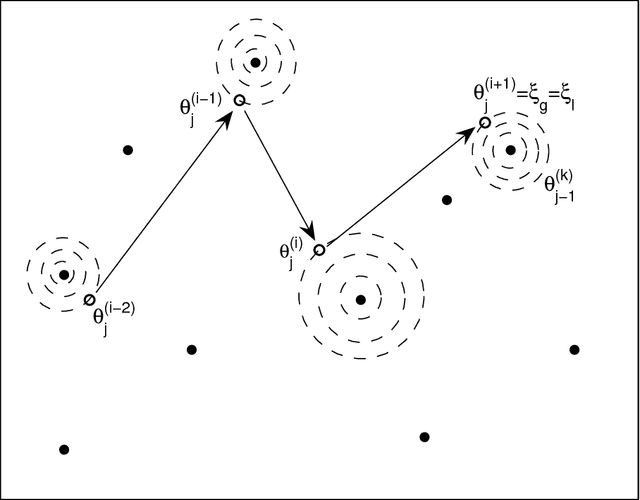
In Bayesian statistics, many problems can be expressed as the evaluation of the expectation of a quantity of interest with respect to the posterior distribution. Standard Monte Carlo method is often not applicable because the encountered posterior distributions cannot be sampled directly. In this case, the most popular strategies are the importance sampling method, Markov chain Monte Carlo, and annealing. In this paper, we introduce a new scheme for Bayesian inference, called Asymptotically Independent Markov Sampling (AIMS), which is based on the above methods. We derive important ergodic properties of AIMS. In particular, it is shown that, under certain conditions, the AIMS algorithm produces a uniformly ergodic Markov chain. The choice of the free parameters of the algorithm is discussed and recommendations are provided for this choice, both theoretically and heuristically based. The efficiency of AIMS is demonstrated with three numerical examples, which include both multi-modal and higher-dimensional target posterior distributions.