Asymptotically Independent Markov Sampling: a new MCMC scheme for Bayesian Inference
Paper and Code
Oct 09, 2011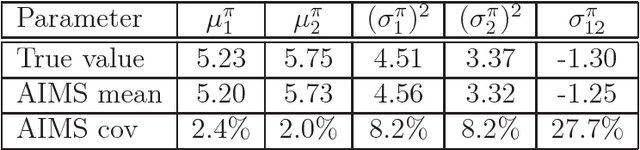
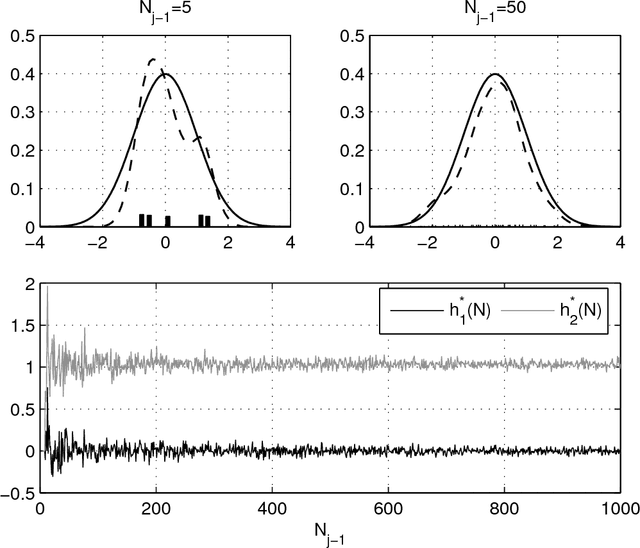
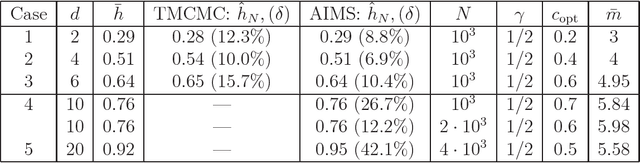
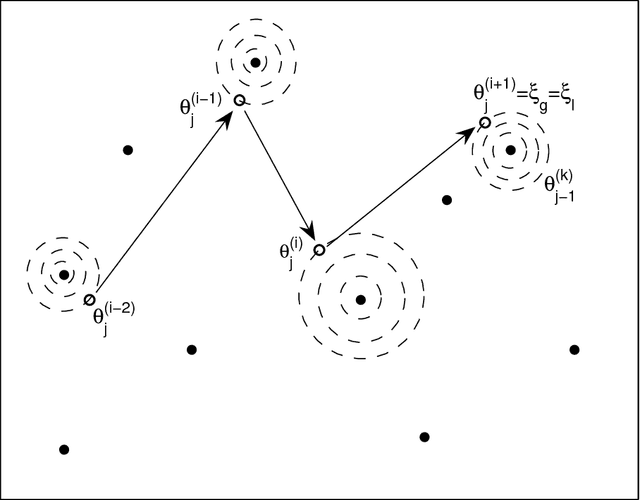
In Bayesian statistics, many problems can be expressed as the evaluation of the expectation of a quantity of interest with respect to the posterior distribution. Standard Monte Carlo method is often not applicable because the encountered posterior distributions cannot be sampled directly. In this case, the most popular strategies are the importance sampling method, Markov chain Monte Carlo, and annealing. In this paper, we introduce a new scheme for Bayesian inference, called Asymptotically Independent Markov Sampling (AIMS), which is based on the above methods. We derive important ergodic properties of AIMS. In particular, it is shown that, under certain conditions, the AIMS algorithm produces a uniformly ergodic Markov chain. The choice of the free parameters of the algorithm is discussed and recommendations are provided for this choice, both theoretically and heuristically based. The efficiency of AIMS is demonstrated with three numerical examples, which include both multi-modal and higher-dimensional target posterior distributions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge