Robust Bayesian compressive sensing with data loss recovery for structural health monitoring signals
Paper and Code
Mar 28, 2015
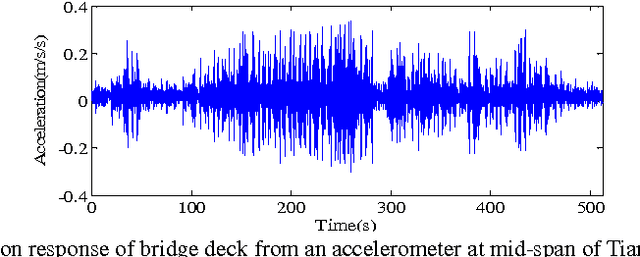
The application of compressive sensing (CS) to structural health monitoring is an emerging research topic. The basic idea in CS is to use a specially-designed wireless sensor to sample signals that are sparse in some basis (e.g. wavelet basis) directly in a compressed form, and then to reconstruct (decompress) these signals accurately using some inversion algorithm after transmission to a central processing unit. However, most signals in structural health monitoring are only approximately sparse, i.e. only a relatively small number of the signal coefficients in some basis are significant, but the other coefficients are usually not exactly zero. In this case, perfect reconstruction from compressed measurements is not expected. A new Bayesian CS algorithm is proposed in which robust treatment of the uncertain parameters is explored, including integration over the prediction-error precision parameter to remove it as a "nuisance" parameter. The performance of the new CS algorithm is investigated using compressed data from accelerometers installed on a space-frame structure and on a cable-stayed bridge. Compared with other state-of-the-art CS methods including our previously-published Bayesian method which uses MAP (maximum a posteriori) estimation of the prediction-error precision parameter, the new algorithm shows superior performance in reconstruction robustness and posterior uncertainty quantification. Furthermore, our method can be utilized for recovery of lost data during wireless transmission, regardless of the level of sparseness in the signal.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge