TEILP: Time Prediction over Knowledge Graphs via Logical Reasoning

Conventional embedding-based models approach event time prediction in temporal knowledge graphs (TKGs) as a ranking problem. However, they often fall short in capturing essential temporal relationships such as order and distance. In this paper, we propose TEILP, a logical reasoning framework that naturaly integrates such temporal elements into knowledge graph predictions. We first convert TKGs into a temporal event knowledge graph (TEKG) which has a more explicit representation of time in term of nodes of the graph. The TEKG equips us to develop a differentiable random walk approach to time prediction. Finally, we introduce conditional probability density functions, associated with the logical rules involving the query interval, using which we arrive at the time prediction. We compare TEILP with state-of-the-art methods on five benchmark datasets. We show that our model achieves a significant improvement over baselines while providing interpretable explanations. In particular, we consider several scenarios where training samples are limited, event types are imbalanced, and forecasting the time of future events based on only past events is desired. In all these cases, TEILP outperforms state-of-the-art methods in terms of robustness.

Temporal Inductive Logic Reasoning

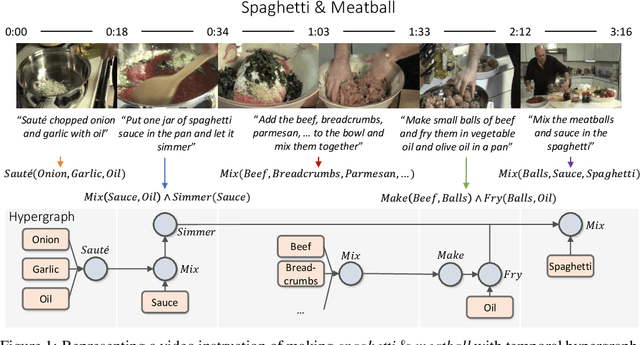
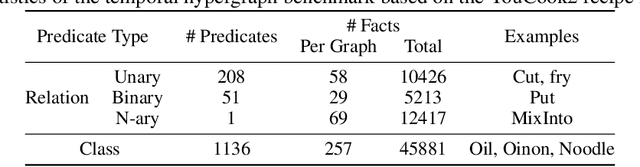
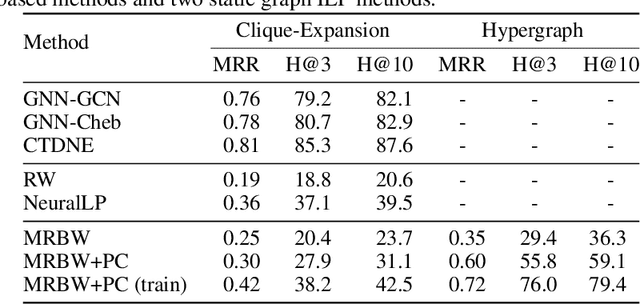
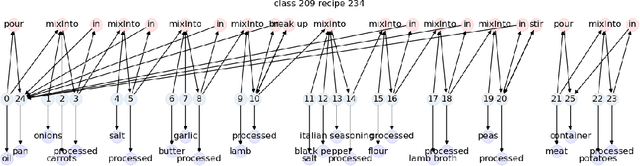
Inductive logic reasoning is one of the fundamental tasks on graphs, which seeks to generalize patterns from the data. This task has been studied extensively for traditional graph datasets such as knowledge graphs (KGs), with representative techniques such as inductive logic programming (ILP). Existing ILP methods typically assume learning from KGs with static facts and binary relations. Beyond KGs, graph structures are widely present in other applications such as video instructions, scene graphs and program executions. While inductive logic reasoning is also beneficial for these applications, applying ILP to the corresponding graphs is nontrivial: they are more complex than KGs, which usually involve timestamps and n-ary relations, effectively a type of hypergraph with temporal events. In this work, we study two of such applications and propose to represent them as hypergraphs with time intervals. To reason on this graph, we propose the multi-start random B-walk that traverses this hypergraph. Combining it with a path-consistency algorithm, we propose an efficient backward-chaining ILP method that learns logic rules by generalizing from both the temporal and the relational data.