Temporal Inductive Logic Reasoning
Paper and Code
Jun 09, 2022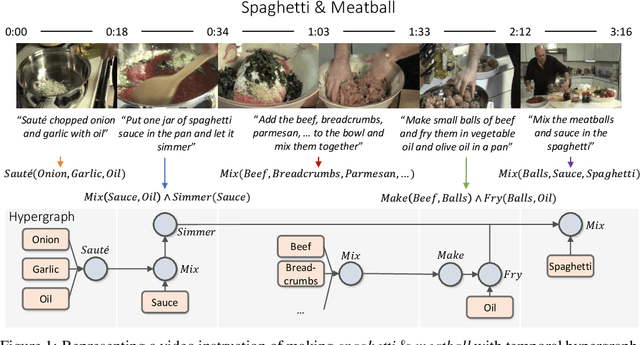
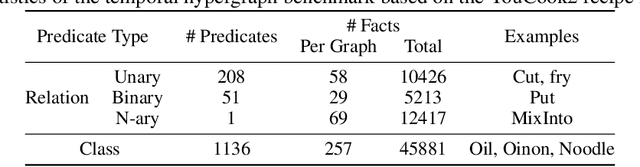
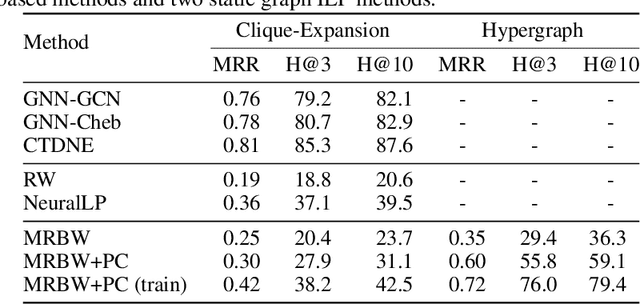
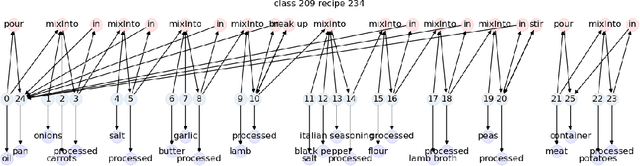
Inductive logic reasoning is one of the fundamental tasks on graphs, which seeks to generalize patterns from the data. This task has been studied extensively for traditional graph datasets such as knowledge graphs (KGs), with representative techniques such as inductive logic programming (ILP). Existing ILP methods typically assume learning from KGs with static facts and binary relations. Beyond KGs, graph structures are widely present in other applications such as video instructions, scene graphs and program executions. While inductive logic reasoning is also beneficial for these applications, applying ILP to the corresponding graphs is nontrivial: they are more complex than KGs, which usually involve timestamps and n-ary relations, effectively a type of hypergraph with temporal events. In this work, we study two of such applications and propose to represent them as hypergraphs with time intervals. To reason on this graph, we propose the multi-start random B-walk that traverses this hypergraph. Combining it with a path-consistency algorithm, we propose an efficient backward-chaining ILP method that learns logic rules by generalizing from both the temporal and the relational data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge