On the relationship between Koopman operator approximations and neural ordinary differential equations for data-driven time-evolution predictions

This work explores the relationship between state space methods and Koopman operator-based methods for predicting the time-evolution of nonlinear dynamical systems. We demonstrate that extended dynamic mode decomposition with dictionary learning (EDMD-DL), when combined with a state space projection, is equivalent to a neural network representation of the nonlinear discrete-time flow map on the state space. We highlight how this projection step introduces nonlinearity into the evolution equations, enabling significantly improved EDMD-DL predictions. With this projection, EDMD-DL leads to a nonlinear dynamical system on the state space, which can be represented in either discrete or continuous time. This system has a natural structure for neural networks, where the state is first expanded into a high dimensional feature space followed by a linear mapping which represents the discrete-time map or the vector field as a linear combination of these features. Inspired by these observations, we implement several variations of neural ordinary differential equations (ODEs) and EDMD-DL, developed by combining different aspects of their respective model structures and training procedures. We evaluate these methods using numerical experiments on chaotic dynamics in the Lorenz system and a nine-mode model of turbulent shear flow, showing comparable performance across methods in terms of short-time trajectory prediction, reconstruction of long-time statistics, and prediction of rare events. We also show that these methods provide comparable performance to a non-Markovian approach in terms of prediction of extreme events.

Stabilization of vertical motion of a vehicle on bumpy terrain using deep reinforcement learning

Stabilizing vertical dynamics for on-road and off-road vehicles is an important research area that has been looked at mostly from the point of view of ride comfort. The advent of autonomous vehicles now shifts the focus more towards developing stabilizing techniques from the point of view of onboard proprioceptive and exteroceptive sensors whose real-time measurements influence the performance of an autonomous vehicle. The current solutions to this problem of managing the vertical oscillations usually limit themselves to the realm of active suspension systems without much consideration to modulating the vehicle velocity, which plays an important role by the virtue of the fact that vertical and longitudinal dynamics of a ground vehicle are coupled. The task of stabilizing vertical oscillations for military ground vehicles becomes even more challenging due lack of structured environments, like city roads or highways, in off-road scenarios. Moreover, changes in structural parameters of the vehicle, such as mass (due to changes in vehicle loading), suspension stiffness and damping values can have significant effect on the controller's performance. This demands the need for developing deep learning based control policies, that can take into account an extremely large number of input features and approximate a near optimal control action. In this work, these problems are addressed by training a deep reinforcement learning agent to minimize the vertical acceleration of a scaled vehicle travelling over bumps by controlling its velocity.

Controlled density transport using Perron Frobenius generators

We consider the problem of the transport of a density of states from an initial state distribution to a desired final state distribution through a dynamical system with actuation. In particular, we consider the case where the control signal is a function of time, but not space; that is, the same actuation is applied at every point in the state space. This is motivated by several problems in fluid mechanics, such as mixing and manipulation of a collection of particles by a global control input such as a uniform magnetic field, as well as by more general control problems where a density function describes an uncertainty distribution or a distribution of agents in a multi-agent system. We formulate this problem using the generators of the Perron-Frobenius operator associated with the drift and control vector fields of the system. By considering finite-dimensional approximations of these operators, the density transport problem can be expressed as a control problem for a bilinear system in a high-dimensional, lifted state. With this system, we frame the density control problem as a problem of driving moments of the density function to the moments of a desired density function, where the moments of the density can be expressed as an output which is linear in the lifted state. This output tracking problem for the lifted bilinear system is then solved using differential dynamic programming, an iterative trajectory optimization scheme.

A Pendulum-Driven Legless Rolling Jumping Robot

In this paper, we present a novel rolling, jumping robot. The robot consists of a driven pendulum mounted to a wheel in a compact, lightweight, 3D printed design. We show that by using the driven pendulum to change it's weight distribution, the robot is able to obtain significant rolling speed, achieve jumps of up to 2.5 body lengths vertically, and also clear horizontal distances of over 6 body lengths while jumping. The robot's dynamic model is derived and simulation results indicate that it is consistent with the motion and jumping observed on the robot. The ability to both roll and jump effectively using a minimalistic design makes this robot unique and could inspire the use of similar mechanisms on robots intended for applications in which agile locomotion on unstructured terrain is necessary, such as disaster response or planetary exploration.

Terrain parameter estimation from proprioceptive sensing of the suspension dynamics in offroad vehicles

Offroad vehicle movement has to contend with uneven and uncertain terrain which present challenges to path planning and motion control for both manned and unmanned ground vehicles. Knowledge of terrain properties can allow a vehicle to adapt its control and motion planning algorithms. Terrain properties, however, can change on time scales of days or even hours, necessitating their online estimation. The kinematics and, in particular the oscillations experienced by an offroad vehicle carry a signature of the terrain properties. These terrain properties can thus be estimated from proprioceptive sensing of the vehicle dynamics with an appropriate model and estimation algorithm. In this paper, we show that knowledge of the vertical dynamics of a vehicle due to its suspension can enable faster and more accurate estimation of terrain parameters. The paper considers a five degree of freedom model that combines the well known half-car and bicycle models. We show through simulation that the sinkage exponent, a parameter that can significantly influence the wheel forces from the terrain and thus greatly impact the vehicle trajectory, can be estimated from measurements of the vehicle's linear acceleration and rotational velocity, which can be readily obtained from an onboard IMU. We show that modelling the vertical vehicle dynamics can lead to significant improvement in both the estimation of terrain parameters and the prediction of the vehicle trajectory.

Magnetically actuated artificial microswimmers as mobile microparticle manipulators

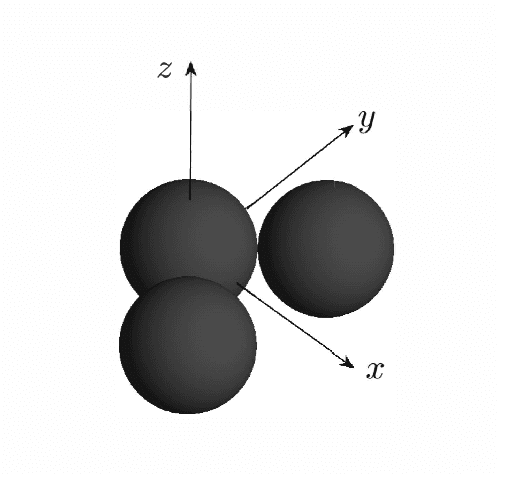
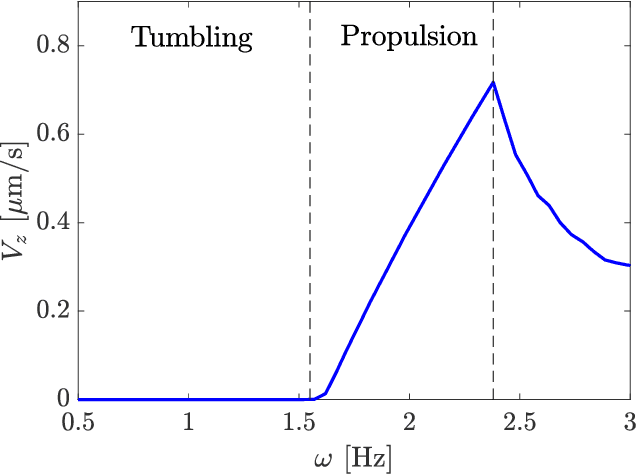
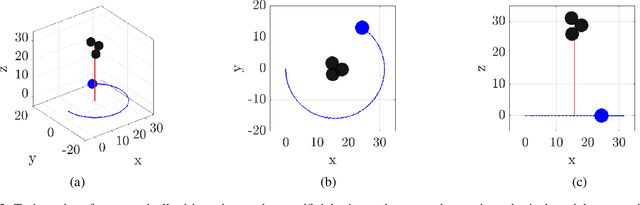
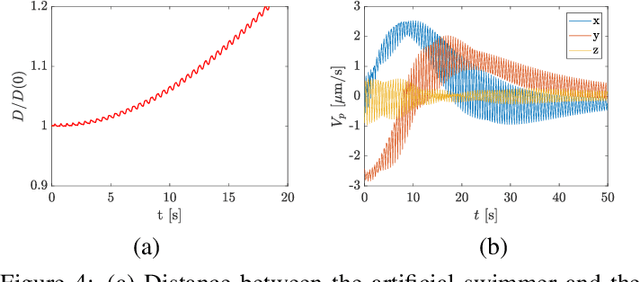
Micro-scale swimming robots have been envisaged for many medical applications such as targeted drug delivery, where the microrobot will be expected to navigate in a fluid through channels carrying a payload. Alternatively, in many cases, such a payload does not have to be physically bound to the swimmer, but may be instead manipulated and steered through the channel by the microrobot. We investigate this problem of contactless manipulation of a microparticle by mobile microswimmer in a fluid at low Reynolds number. We consider a model of a magnetically actuated artificial microswimmer, whose locomotion through a fluid induces a disturbance velocity field in the fluid, that then acts to propel a cargo particle in its vicinity. The problem investigated in this paper is therefore one of coupled locomotion-manipulation of two bodies in a fluid. The magnetic swimmer's motion is actuated by an externally applied magnetic field of constant strength but whose direction rotates at a constant rate in a plane. The swimmer propels itself in the direction perpendicular to this plane if the frequency associated with the periodic magnetic field is above a critical frequency. Below this critical frequency, the swimmer tumbles in place without net locomotion. The coupled fluid-swimmer-cargo particle dynamics are solved numerically using the method of Stokesian dynamics. The induced motion of the cargo particle is shown to be controllable. This is achieved by switching the planes of rotation of the magnetic field and switching frequency of the magnetic field above and below the critical frequency. While a swimmer with a specific geometry has been used in the model, the results of this paper are applicable to swimmers with other geometries and means of propulsion. The results of this paper show that microswimmers can be utilized as mobile manipulators of microparticles in a fluid.