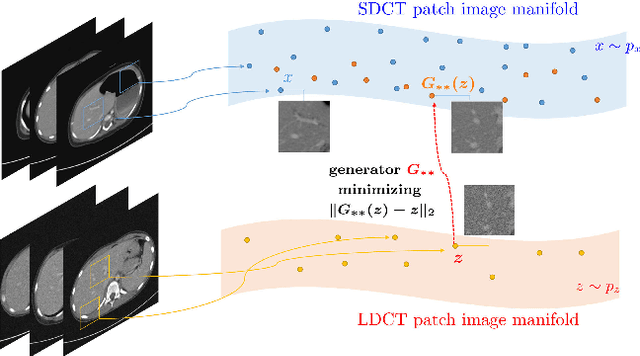
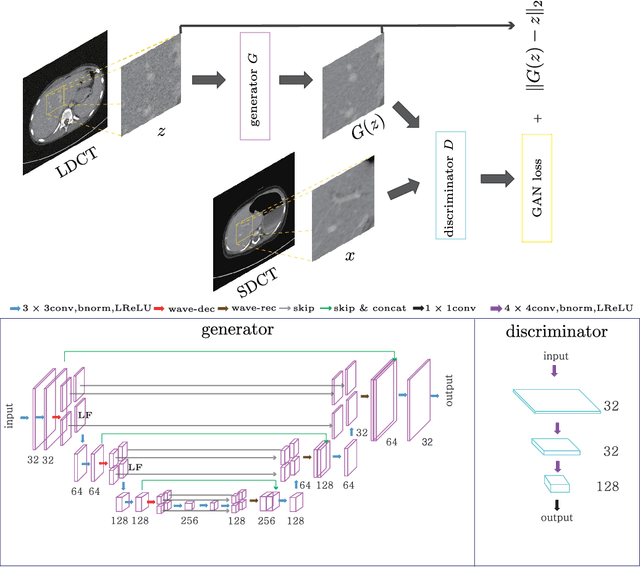
Unpaired image denoising using a generative adversarial network in X-ray CT

This paper proposes a deep learning-based denoising method for noisy low-dose computerized tomography (CT) images in the absence of paired training data. The proposed method uses a fidelity-embedded generative adversarial network (GAN) to learn a denoising function from unpaired training data of low-dose CT (LDCT) and standard-dose CT (SDCT) images, where the denoising function is the optimal generator in the GAN framework. Given an optimal discriminator in the GAN, the generator is optimized by minimizing a weighted sum of two losses: the Kullback-Leibler divergence between an SDCT data distribution and a generated distribution, and the $\ell_2$ loss between the LDCT image and the corresponding generated images (or denoised image). The experimental results show that the proposed deep-learning method with unpaired datasets performs comparably to a method using paired datasets. Clinical experiment was also performed to show the validity of the proposed method for non-Gaussian noise arising in the low-dose X-ray CT.

Whole Brain Susceptibility Mapping Using Harmonic Incompatibility Removal

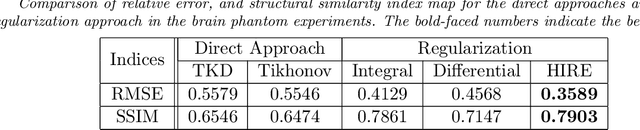
Quantitative susceptibility mapping (QSM) uses the phase data in magnetic resonance signal to visualize a three dimensional susceptibility distribution by solving the magnetic field to susceptibility inverse problem. Due to the presence of zeros of the integration kernel in the frequency domain, QSM is an ill-posed inverse problem. Although numerous regularization based models have been proposed to overcome this problem, the incompatibility in the field data has not received enough attention, which leads to deterioration of the recovery. In this paper, we show that the data acquisition process of QSM inherently generates a harmonic incompatibility in the measured local field. Based on such discovery, we propose a novel regularization based susceptibility reconstruction model with an additional sparsity based regularization term on the harmonic incompatibility. Numerical experiments show that the proposed method achieves better performance than the existing approaches.

An Edge Driven Wavelet Frame Model for Image Restoration

Wavelet frame systems are known to be effective in capturing singularities from noisy and degraded images. In this paper, we introduce a new edge driven wavelet frame model for image restoration by approximating images as piecewise smooth functions. With an implicit representation of image singularities sets, the proposed model inflicts different strength of regularization on smooth and singular image regions and edges. The proposed edge driven model is robust to both image approximation and singularity estimation. The implicit formulation also enables an asymptotic analysis of the proposed models and a rigorous connection between the discrete model and a general continuous variational model. Finally, numerical results on image inpainting and deblurring show that the proposed model is compared favorably against several popular image restoration models.