Whole Brain Susceptibility Mapping Using Harmonic Incompatibility Removal

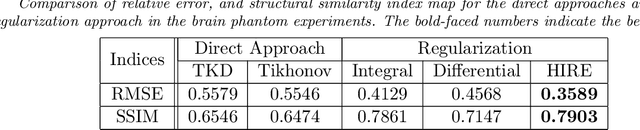
Quantitative susceptibility mapping (QSM) uses the phase data in magnetic resonance signal to visualize a three dimensional susceptibility distribution by solving the magnetic field to susceptibility inverse problem. Due to the presence of zeros of the integration kernel in the frequency domain, QSM is an ill-posed inverse problem. Although numerous regularization based models have been proposed to overcome this problem, the incompatibility in the field data has not received enough attention, which leads to deterioration of the recovery. In this paper, we show that the data acquisition process of QSM inherently generates a harmonic incompatibility in the measured local field. Based on such discovery, we propose a novel regularization based susceptibility reconstruction model with an additional sparsity based regularization term on the harmonic incompatibility. Numerical experiments show that the proposed method achieves better performance than the existing approaches.