Slim multi-scale convolutional autoencoder-based reduced-order models for interpretable features of a complex dynamical system

In recent years, data-driven deep learning models have gained significant interest in the analysis of turbulent dynamical systems. Within the context of reduced-order models (ROMs), convolutional autoencoders (CAEs) pose a universally applicable alternative to conventional approaches. They can learn nonlinear transformations directly from data, without prior knowledge of the system. However, the features generated by such models lack interpretability. Thus, the resulting model is a black-box which effectively reduces the complexity of the system, but does not provide insights into the meaning of the latent features. To address this critical issue, we introduce a novel interpretable CAE approach for high-dimensional fluid flow data that maintains the reconstruction quality of conventional CAEs and allows for feature interpretation. Our method can be easily integrated into any existing CAE architecture with minor modifications of the training process. We compare our approach to Proper Orthogonal Decomposition (POD) and two existing methods for interpretable CAEs. We apply all methods to three different experimental turbulent Rayleigh-B\'enard convection datasets with varying complexity. Our results show that the proposed method is lightweight, easy to train, and achieves relative reconstruction performance improvements of up to 6.4% over POD for 64 modes. The relative improvement increases to up to 229.8% as the number of modes decreases. Additionally, our method delivers interpretable features similar to those of POD and is significantly less resource-intensive than existing CAE approaches, using less than 2% of the parameters. These approaches either trade interpretability for reconstruction performance or only provide interpretability to a limited extend.

Asymmetrically connected reservoir networks learn better

We show that connectivity within the high-dimensional recurrent layer of a reservoir network is crucial for its performance. To this end, we systematically investigate the impact of network connectivity on its performance, i.e., we examine the symmetry and structure of the reservoir in relation to its computational power. Reservoirs with random and asymmetric connections are found to perform better for an exemplary Mackey-Glass time series than all structured reservoirs, including biologically inspired connectivities, such as small-world topologies. This result is quantified by the information processing capacity of the different network topologies which becomes highest for asymmetric and randomly connected networks.

Generative convective parametrization of dry atmospheric boundary layer

Turbulence parametrizations will remain a necessary building block in kilometer-scale Earth system models. In convective boundary layers, where the mean vertical gradients of conserved properties such as potential temperature and moisture are approximately zero, the standard ansatz which relates turbulent fluxes to mean vertical gradients via an eddy diffusivity has to be extended by mass flux parametrizations for the typically asymmetric up- and downdrafts in the atmospheric boundary layer. In this work, we present a parametrization for a dry convective boundary layer based on a generative adversarial network. The model incorporates the physics of self-similar layer growth following from the classical mixed layer theory by Deardorff. This enhances the training data base of the generative machine learning algorithm and thus significantly improves the predicted statistics of the synthetically generated turbulence fields at different heights inside the boundary layer. The algorithm training is based on fully three-dimensional direct numerical simulation data. Differently to stochastic parametrizations, our model is able to predict the highly non-Gaussian transient statistics of buoyancy fluctuations, vertical velocity, and buoyancy flux at different heights thus also capturing the fastest thermals penetrating into the stabilized top region. The results of our generative algorithm agree with standard two-equation or multi-plume stochastic mass-flux schemes. The present parametrization provides additionally the granule-type horizontal organization of the turbulent convection which cannot be obtained in any of the other model closures. Our work paves the way to efficient data-driven convective parametrizations in other natural flows, such as moist convection, upper ocean mixing, or convection in stellar interiors.

Direct data-driven forecast of local turbulent heat flux in Rayleigh-Bénard convection

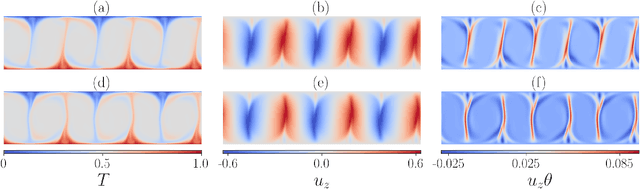
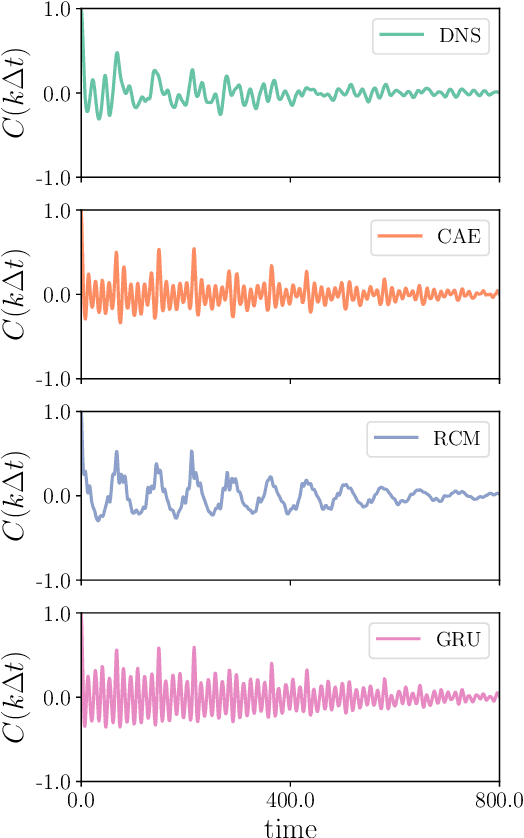
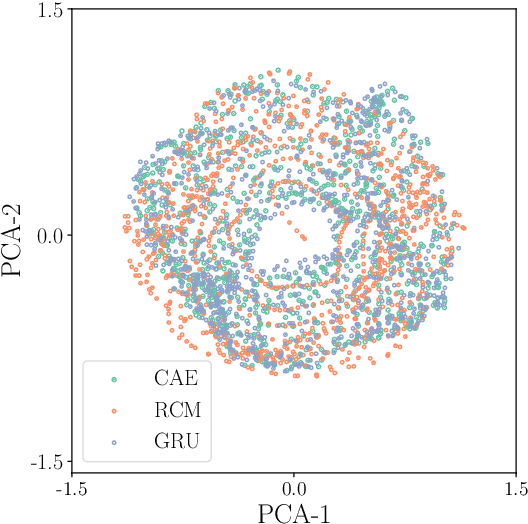
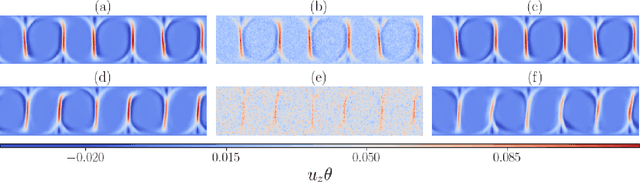
A combined convolutional autoencoder-recurrent neural network machine learning model is presented to analyse and forecast the dynamics and low-order statistics of the local convective heat flux field in a two-dimensional turbulent Rayleigh-B\'{e}nard convection flow at Prandtl number ${\rm Pr}=7$ and Rayleigh number ${\rm Ra}=10^7$. Two recurrent neural networks are applied for the temporal advancement of flow data in the reduced latent data space, a reservoir computing model in the form of an echo state network and a recurrent gated unit. Thereby, the present work exploits the modular combination of three different machine learning algorithms to build a fully data-driven and reduced model for the dynamics of the turbulent heat transfer in a complex thermally driven flow. The convolutional autoencoder with 12 hidden layers is able to reduce the dimensionality of the turbulence data to about 0.2 \% of their original size. Our results indicate a fairly good accuracy in the first- and second-order statistics of the convective heat flux. The algorithm is also able to reproduce the intermittent plume-mixing dynamics at the upper edges of the thermal boundary layers with some deviations. The same holds for the probability density function of the local convective heat flux with differences in the far tails. Furthermore, we demonstrate the noise resilience of the framework which suggests the present model might be applicable as a reduced dynamical model that delivers transport fluxes and their variations to the coarse grid cells of larger-scale computational models, such as global circulation models for the atmosphere and ocean.

Echo State Network for two-dimensional turbulent moist Rayleigh-Bénard convection

Recurrent neural networks are machine learning algorithms which are suited well to predict time series. Echo state networks are one specific implementation of such neural networks that can describe the evolution of dynamical systems by supervised machine learning without solving the underlying nonlinear mathematical equations. In this work, we apply an echo state network to approximate the evolution of two-dimensional moist Rayleigh-B\'enard convection and the resulting low-order turbulence statistics. We conduct long-term direct numerical simulations in order to obtain training and test data for the algorithm. Both sets are pre-processed by a Proper Orthogonal Decomposition (POD) using the snapshot method to reduce the amount of data. The training data comprise long time series of the first 150 most energetic POD coefficients. The reservoir is subsequently fed by the data and results in predictions of future flow states. The predictions are thoroughly validated by the data of the original simulation. Our results show good agreement of the low-order statistics. This incorporates also derived statistical moments such as the cloud cover close to the top of the convection layer and the flux of liquid water across the domain. We conclude that our model is capable of learning complex dynamics which is introduced here by the tight interaction of turbulence with the nonlinear thermodynamics of phase changes between vapor and liquid water. Our work opens new ways for the dynamic parametrization of subgrid-scale transport in larger-scale circulation models.

Reservoir computing model of two-dimensional turbulent convection

Reservoir computing is applied to model the large-scale evolution and the resulting low-order turbulence statistics of a two-dimensional turbulent Rayleigh-B\'{e}nard convection flow at a Rayleigh number ${\rm Ra}=10^7$ and a Prandtl number ${\rm Pr}=7$ in an extended domain with an aspect ratio of 6. Our data-driven approach which is based on a long-term direct numerical simulation of the convection flow comprises a two-step procedure. (1) Reduction of the original simulation data by a Proper Orthogonal Decomposition (POD) snapshot analysis and subsequent truncation to the first 150 POD modes which are associated with the largest total energy amplitudes. (2) Setup and optimization of a reservoir computing model to describe the dynamical evolution of these 150 degrees of freedom and thus the large-scale evolution of the convection flow. The quality of the prediction of the reservoir computing model is comprehensively tested. At the core of the model is the reservoir, a very large sparse random network charcterized by the spectral radius of the corresponding adjacency matrix and a few further hyperparameters which are varied to investigate the quality of the prediction. Our work demonstrates that the reservoir computing model is capable to model the large-scale structure and low-order statistics of turbulent convection which can open new avenues for modeling mesoscale convection processes in larger circulation models.