Direct data-driven forecast of local turbulent heat flux in Rayleigh-Bénard convection

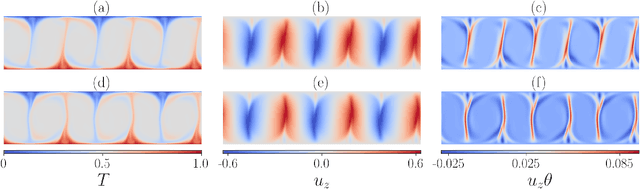
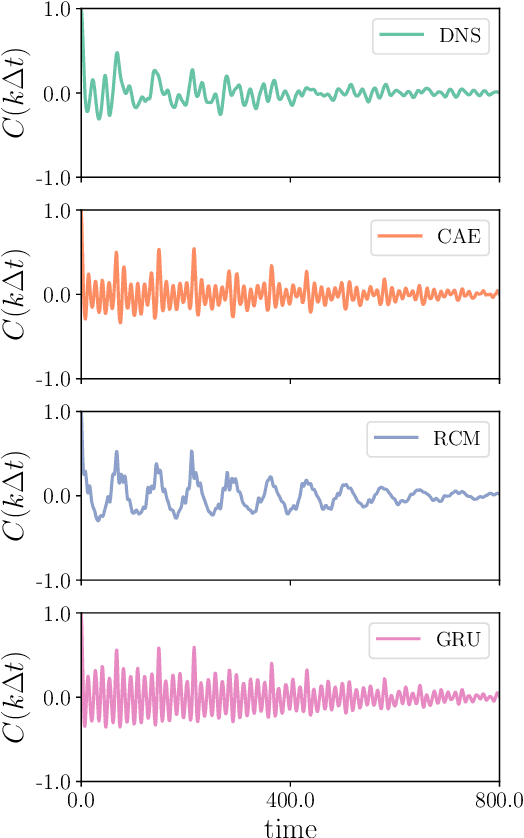
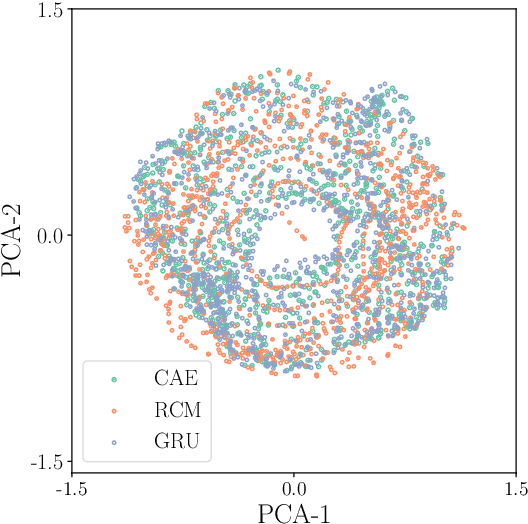
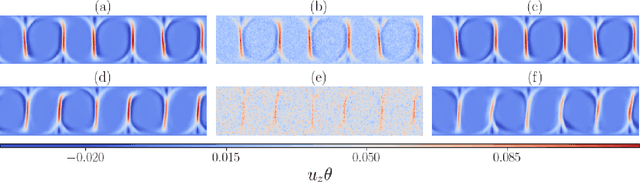
A combined convolutional autoencoder-recurrent neural network machine learning model is presented to analyse and forecast the dynamics and low-order statistics of the local convective heat flux field in a two-dimensional turbulent Rayleigh-B\'{e}nard convection flow at Prandtl number ${\rm Pr}=7$ and Rayleigh number ${\rm Ra}=10^7$. Two recurrent neural networks are applied for the temporal advancement of flow data in the reduced latent data space, a reservoir computing model in the form of an echo state network and a recurrent gated unit. Thereby, the present work exploits the modular combination of three different machine learning algorithms to build a fully data-driven and reduced model for the dynamics of the turbulent heat transfer in a complex thermally driven flow. The convolutional autoencoder with 12 hidden layers is able to reduce the dimensionality of the turbulence data to about 0.2 \% of their original size. Our results indicate a fairly good accuracy in the first- and second-order statistics of the convective heat flux. The algorithm is also able to reproduce the intermittent plume-mixing dynamics at the upper edges of the thermal boundary layers with some deviations. The same holds for the probability density function of the local convective heat flux with differences in the far tails. Furthermore, we demonstrate the noise resilience of the framework which suggests the present model might be applicable as a reduced dynamical model that delivers transport fluxes and their variations to the coarse grid cells of larger-scale computational models, such as global circulation models for the atmosphere and ocean.

Reservoir computing model of two-dimensional turbulent convection

Reservoir computing is applied to model the large-scale evolution and the resulting low-order turbulence statistics of a two-dimensional turbulent Rayleigh-B\'{e}nard convection flow at a Rayleigh number ${\rm Ra}=10^7$ and a Prandtl number ${\rm Pr}=7$ in an extended domain with an aspect ratio of 6. Our data-driven approach which is based on a long-term direct numerical simulation of the convection flow comprises a two-step procedure. (1) Reduction of the original simulation data by a Proper Orthogonal Decomposition (POD) snapshot analysis and subsequent truncation to the first 150 POD modes which are associated with the largest total energy amplitudes. (2) Setup and optimization of a reservoir computing model to describe the dynamical evolution of these 150 degrees of freedom and thus the large-scale evolution of the convection flow. The quality of the prediction of the reservoir computing model is comprehensively tested. At the core of the model is the reservoir, a very large sparse random network charcterized by the spectral radius of the corresponding adjacency matrix and a few further hyperparameters which are varied to investigate the quality of the prediction. Our work demonstrates that the reservoir computing model is capable to model the large-scale structure and low-order statistics of turbulent convection which can open new avenues for modeling mesoscale convection processes in larger circulation models.