A Scalable System for Visual Analysis of Ocean Data

Oceanographers rely on visual analysis to interpret model simulations, identify events and phenomena, and track dynamic ocean processes. The ever increasing resolution and complexity of ocean data due to its dynamic nature and multivariate relationships demands a scalable and adaptable visualization tool for interactive exploration. We introduce pyParaOcean, a scalable and interactive visualization system designed specifically for ocean data analysis. pyParaOcean offers specialized modules for common oceanographic analysis tasks, including eddy identification and salinity movement tracking. These modules seamlessly integrate with ParaView as filters, ensuring a user-friendly and easy-to-use system while leveraging the parallelization capabilities of ParaView and a plethora of inbuilt general-purpose visualization functionalities. The creation of an auxiliary dataset stored as a Cinema database helps address I/O and network bandwidth bottlenecks while supporting the generation of quick overview visualizations. We present a case study on the Bay of Bengal (BoB) to demonstrate the utility of the system and scaling studies to evaluate the efficiency of the system.

Multi-field Visualization: Trait design and trait-induced merge trees

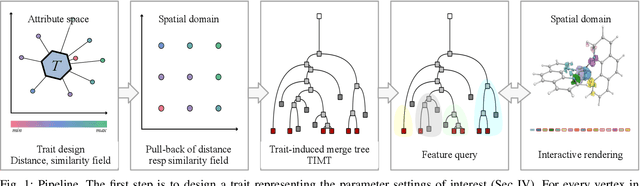
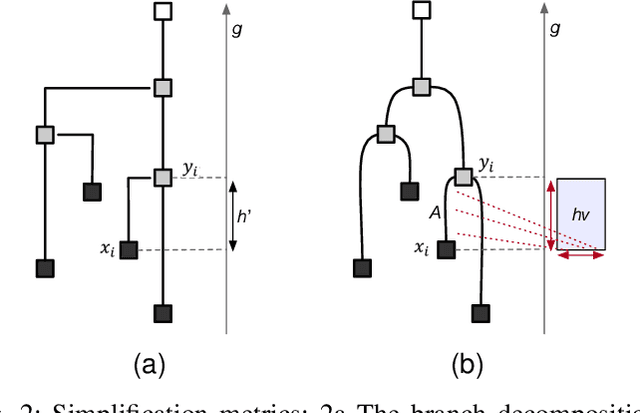
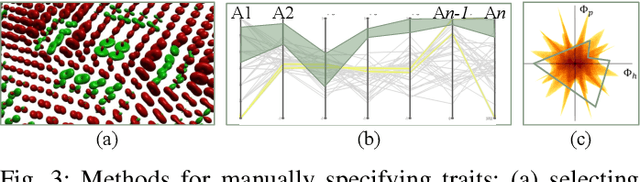
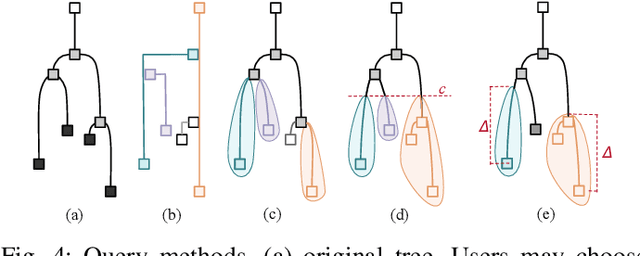
Feature level sets (FLS) have shown significant potential in the analysis of multi-field data by using traits defined in attribute space to specify features in the domain. In this work, we address key challenges in the practical use of FLS: trait design and feature selection for rendering. To simplify trait design, we propose a Cartesian decomposition of traits into simpler components, making the process more intuitive and computationally efficient. Additionally, we utilize dictionary learning results to automatically suggest point traits. To enhance feature selection, we introduce trait-induced merge trees (TIMTs), a generalization of merge trees for feature level sets, aimed at topologically analyzing tensor fields or general multi-variate data. The leaves in the TIMT represent areas in the input data that are closest to the defined trait, thereby most closely resembling the defined feature. This merge tree provides a hierarchy of features, enabling the querying of the most relevant and persistent features. Our method includes various query techniques for the tree, allowing the highlighting of different aspects. We demonstrate the cross-application capabilities of this approach through five case studies from different domains.

Multi-scale Cycle Tracking in Dynamic Planar Graphs

This paper presents a nested tracking framework for analyzing cycles in 2D force networks within granular materials. These materials are composed of interacting particles, whose interactions are described by a force network. Understanding the cycles within these networks at various scales and their evolution under external loads is crucial, as they significantly contribute to the mechanical and kinematic properties of the system. Our approach involves computing a cycle hierarchy by partitioning the 2D domain into segments bounded by cycles in the force network. We can adapt concepts from nested tracking graphs originally developed for merge trees by leveraging the duality between this partitioning and the cycles. We demonstrate the effectiveness of our method on two force networks derived from experiments with photoelastic disks.

Multi-field Visualisation via Trait-induced Merge Trees

In this work, we propose trait-based merge trees a generalization of merge trees to feature level sets, targeting the analysis of tensor field or general multi-variate data. For this, we employ the notion of traits defined in attribute space as introduced in the feature level sets framework. The resulting distance field in attribute space induces a scalar field in the spatial domain that serves as input for topological data analysis. The leaves in the merge tree represent those areas in the input data that are closest to the defined trait and thus most closely resemble the defined feature. Hence, the merge tree yields a hierarchy of features that allows for querying the most relevant and persistent features. The presented method includes different query methods for the tree which enable the highlighting of different aspects. We demonstrate the cross-application capabilities of this approach with three case studies from different domains.

Combinatorial Gradient Fields for 2D Images with Empirically Convergent Separatrices

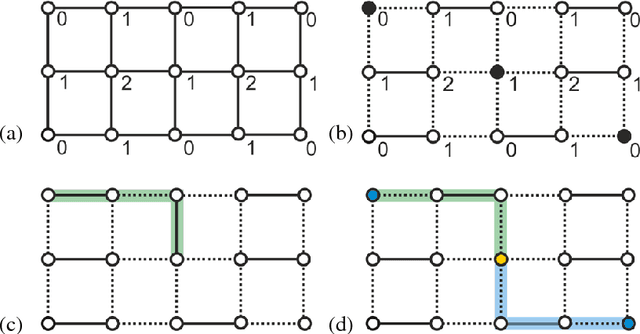
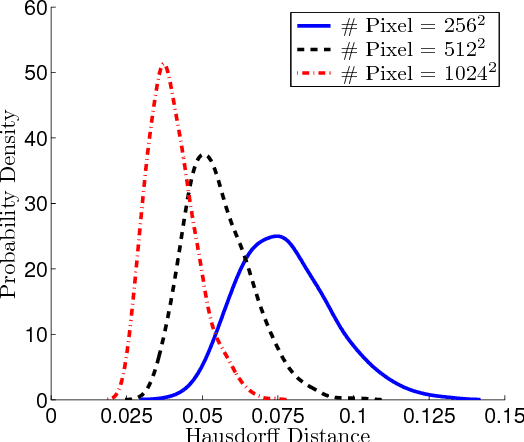
This paper proposes an efficient probabilistic method that computes combinatorial gradient fields for two dimensional image data. In contrast to existing algorithms, this approach yields a geometric Morse-Smale complex that converges almost surely to its continuous counterpart when the image resolution is increased. This approach is motivated using basic ideas from probability theory and builds upon an algorithm from discrete Morse theory with a strong mathematical foundation. While a formal proof is only hinted at, we do provide a thorough numerical evaluation of our method and compare it to established algorithms.