A Rate-Distortion View of Uncertainty Quantification

In supervised learning, understanding an input's proximity to the training data can help a model decide whether it has sufficient evidence for reaching a reliable prediction. While powerful probabilistic models such as Gaussian Processes naturally have this property, deep neural networks often lack it. In this paper, we introduce Distance Aware Bottleneck (DAB), i.e., a new method for enriching deep neural networks with this property. Building on prior information bottleneck approaches, our method learns a codebook that stores a compressed representation of all inputs seen during training. The distance of a new example from this codebook can serve as an uncertainty estimate for the example. The resulting model is simple to train and provides deterministic uncertainty estimates by a single forward pass. Finally, our method achieves better out-of-distribution (OOD) detection and misclassification prediction than prior methods, including expensive ensemble methods, deep kernel Gaussian Processes, and approaches based on the standard information bottleneck.

Self-Reflective Variational Autoencoder

The Variational Autoencoder (VAE) is a powerful framework for learning probabilistic latent variable generative models. However, typical assumptions on the approximate posterior distribution of the encoder and/or the prior, seriously restrict its capacity for inference and generative modeling. Variational inference based on neural autoregressive models respects the conditional dependencies of the exact posterior, but this flexibility comes at a cost: such models are expensive to train in high-dimensional regimes and can be slow to produce samples. In this work, we introduce an orthogonal solution, which we call self-reflective inference. By redesigning the hierarchical structure of existing VAE architectures, self-reflection ensures that the stochastic flow preserves the factorization of the exact posterior, sequentially updating the latent codes in a recurrent manner consistent with the generative model. We empirically demonstrate the clear advantages of matching the variational posterior to the exact posterior - on binarized MNIST, self-reflective inference achieves state-of-the art performance without resorting to complex, computationally expensive components such as autoregressive layers. Moreover, we design a variational normalizing flow that employs the proposed architecture, yielding predictive benefits compared to its purely generative counterpart. Our proposed modification is quite general and complements the existing literature; self-reflective inference can naturally leverage advances in distribution estimation and generative modeling to improve the capacity of each layer in the hierarchy.

Tractable Learning and Inference for Large-Scale Probabilistic Boolean Networks

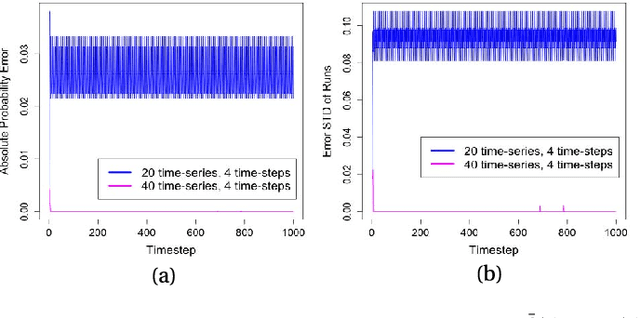
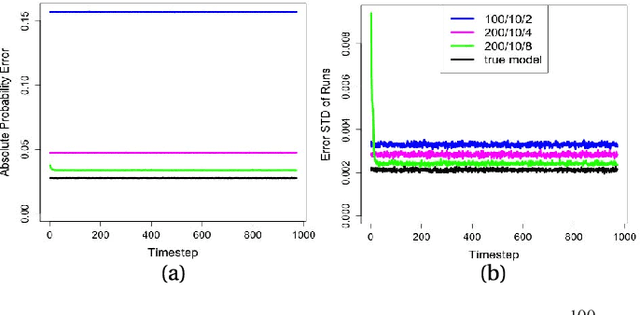
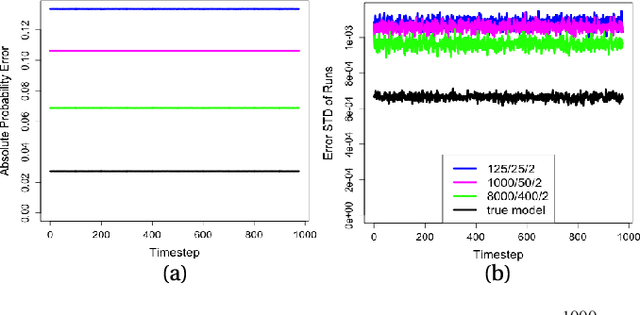
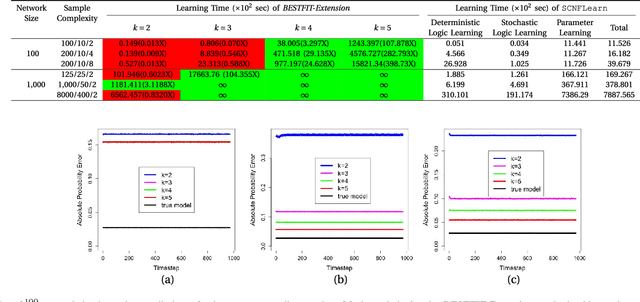
Probabilistic Boolean Networks (PBNs) have been previously proposed so as to gain insights into complex dy- namical systems. However, identification of large networks and of the underlying discrete Markov Chain which describes their temporal evolution, still remains a challenge. In this paper, we introduce an equivalent representation for the PBN, the Stochastic Conjunctive Normal Form (SCNF), which paves the way to a scalable learning algorithm and helps predict long- run dynamic behavior of large-scale systems. Moreover, SCNF allows its efficient sampling so as to statistically infer multi- step transition probabilities which can provide knowledge on the activity levels of individual nodes in the long run.