Tractable Learning and Inference for Large-Scale Probabilistic Boolean Networks
Paper and Code
Jan 23, 2018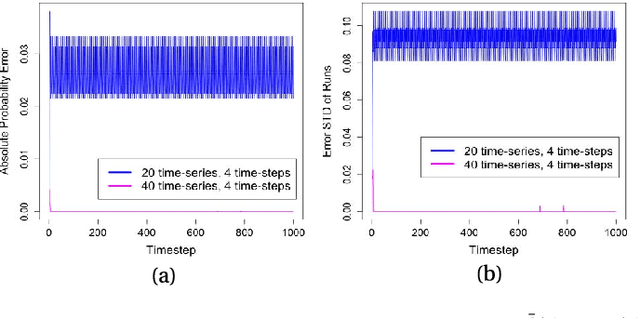
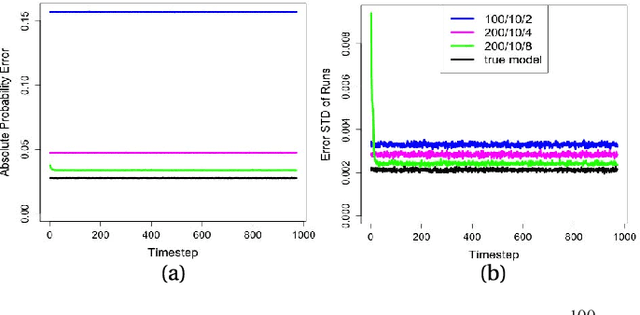
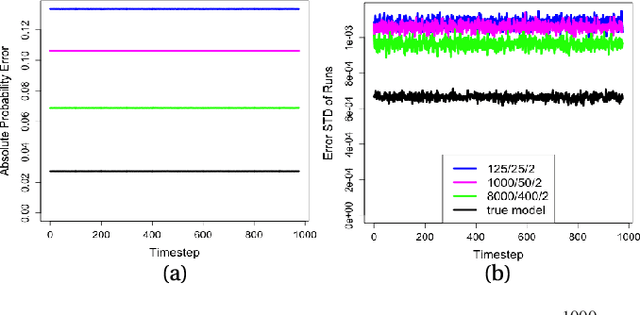
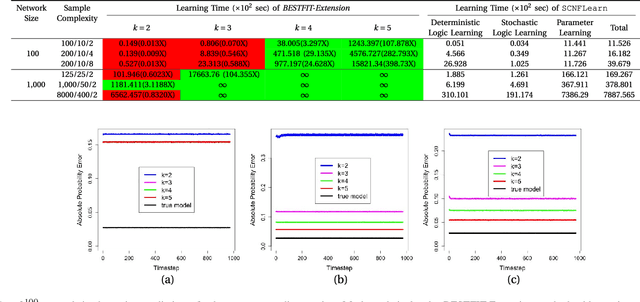
Probabilistic Boolean Networks (PBNs) have been previously proposed so as to gain insights into complex dy- namical systems. However, identification of large networks and of the underlying discrete Markov Chain which describes their temporal evolution, still remains a challenge. In this paper, we introduce an equivalent representation for the PBN, the Stochastic Conjunctive Normal Form (SCNF), which paves the way to a scalable learning algorithm and helps predict long- run dynamic behavior of large-scale systems. Moreover, SCNF allows its efficient sampling so as to statistically infer multi- step transition probabilities which can provide knowledge on the activity levels of individual nodes in the long run.
* 16 pages
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge