Imperialist Competitive Algorithm with Independence and Constrained Assimilation for Solving 0-1 Multidimensional Knapsack Problem

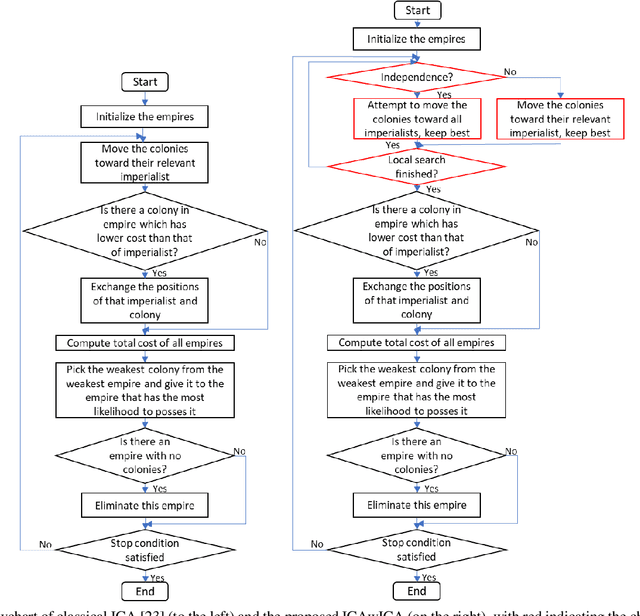
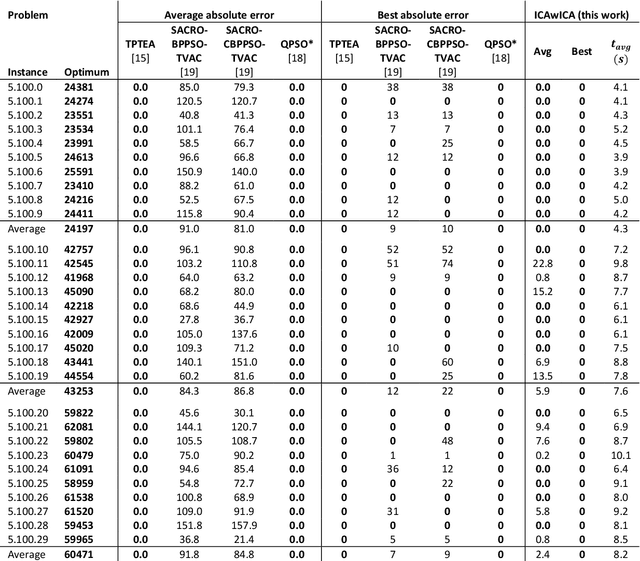
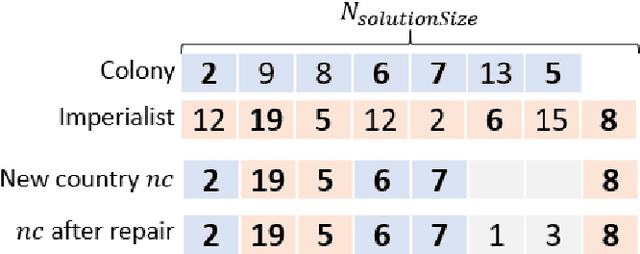
The multidimensional knapsack problem is a well-known constrained optimization problem with many real-world engineering applications. In order to solve this NP-hard problem, a new modified Imperialist Competitive Algorithm with Constrained Assimilation (ICAwICA) is presented. The proposed algorithm introduces the concept of colony independence, a free will to choose between classical ICA assimilation to empires imperialist or any other imperialist in the population. Furthermore, a constrained assimilation process has been implemented that combines classical ICA assimilation and revolution operators, while maintaining population diversity. This work investigates the performance of the proposed algorithm across 101 Multidimensional Knapsack Problem (MKP) benchmark instances. Experimental results show that the algorithm is able to obtain an optimal solution in all small instances and presents very competitive results for large MKP instances.

Dynamic Impact for Ant Colony Optimization algorithm

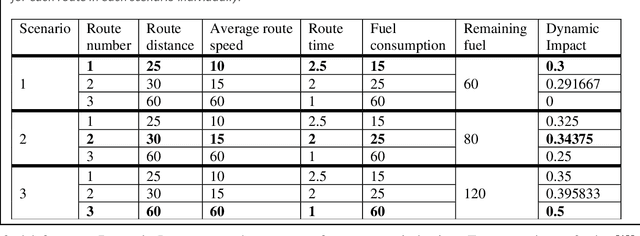
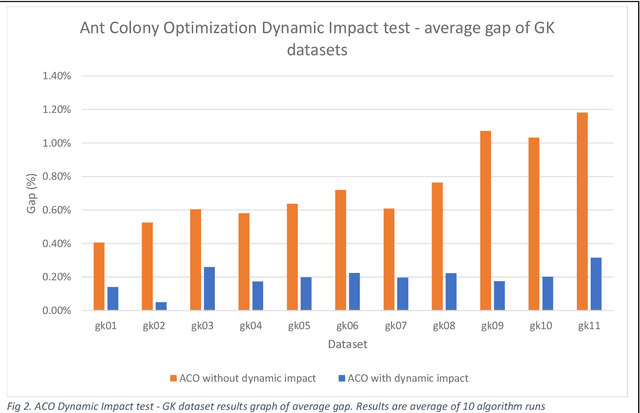
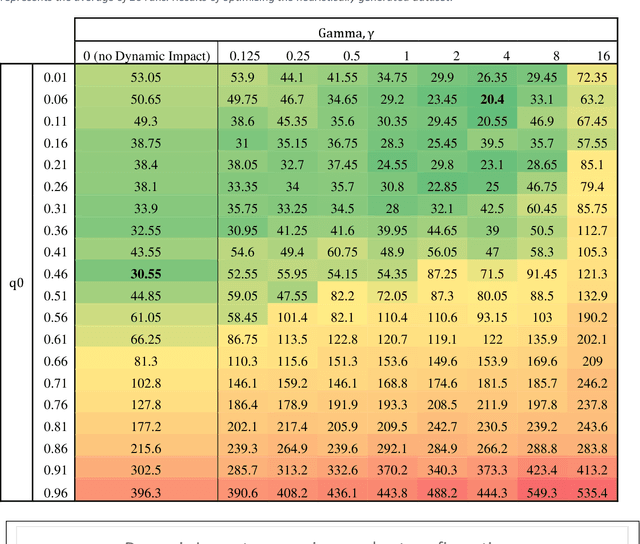
This paper proposes an extension method for Ant Colony Optimization (ACO) algorithm called Dynamic Impact. Dynamic Impact is designed to solve challenging optimization problems that has nonlinear relationship between resource consumption and fitness in relation to other part of the optimized solution. This proposed method is tested against complex real-world Microchip Manufacturing Plant Production Floor Optimization (MMPPFO) problem, as well as theoretical benchmark Multi-Dimensional Knapsack problem (MKP). MMPPFO is a non-trivial optimization problem, due the nature of solution fitness value dependence on collection of wafer-lots without prioritization of any individual wafer-lot. Using Dynamic Impact on single objective optimization fitness value is improved by 33.2%. Furthermore, MKP benchmark instances of small complexity have been solved to 100% success rate where high degree of solution sparseness is observed, and large instances have showed average gap improved by 4.26 times. Algorithm implementation demonstrated superior performance across small and large datasets and sparse optimization problems.

A Branching and Merging Convolutional Network with Homogeneous Filter Capsules

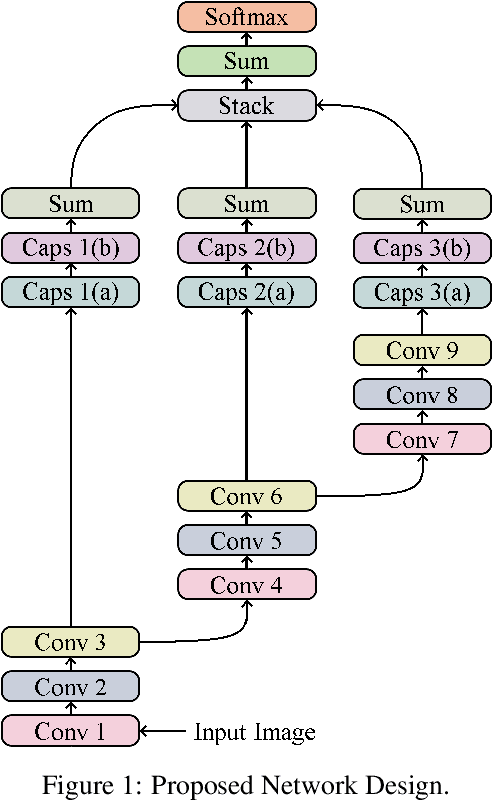
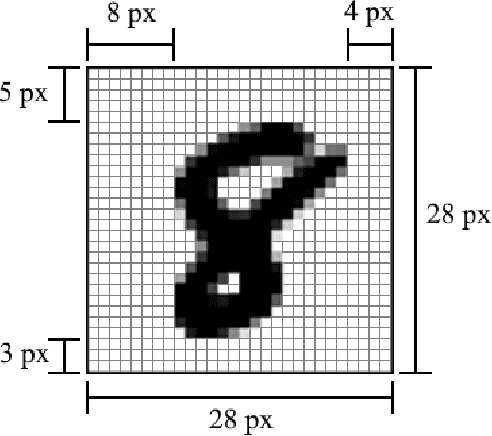
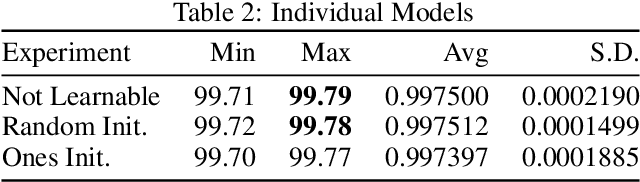
We present a convolutional neural network design with additional branches after certain convolutions so that we can extract features with differing effective receptive fields and levels of abstraction. From each branch, we transform each of the final filters into a pair of homogeneous vector capsules. As the capsules are formed from entire filters, we refer to them as filter capsules. We then compare three methods for merging the branches--merging with equal weight and merging with learned weights, with two different weight initialization strategies. This design, in combination with a domain-specific set of randomly applied augmentation techniques, establishes a new state of the art for the MNIST dataset with an accuracy of 99.84% for an ensemble of these models, as well as establishing a new state of the art for a single model (99.79% accurate). These accuracies were achieved with a 75% reduction in both the number of parameters and the number of epochs of training relative to the previously best performing capsule network on MNIST. All training was performed using the Adam optimizer and experienced no overfitting.