A Branching and Merging Convolutional Network with Homogeneous Filter Capsules
Paper and Code
Jan 31, 2020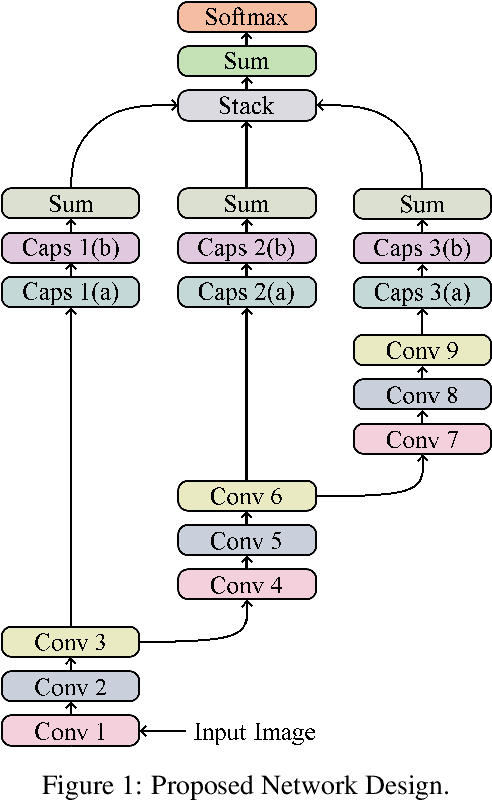

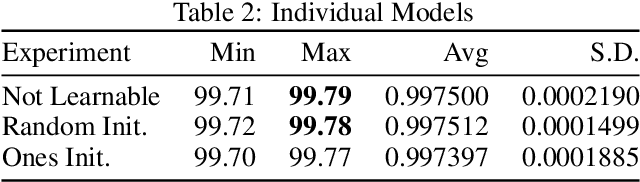
We present a convolutional neural network design with additional branches after certain convolutions so that we can extract features with differing effective receptive fields and levels of abstraction. From each branch, we transform each of the final filters into a pair of homogeneous vector capsules. As the capsules are formed from entire filters, we refer to them as filter capsules. We then compare three methods for merging the branches--merging with equal weight and merging with learned weights, with two different weight initialization strategies. This design, in combination with a domain-specific set of randomly applied augmentation techniques, establishes a new state of the art for the MNIST dataset with an accuracy of 99.84% for an ensemble of these models, as well as establishing a new state of the art for a single model (99.79% accurate). These accuracies were achieved with a 75% reduction in both the number of parameters and the number of epochs of training relative to the previously best performing capsule network on MNIST. All training was performed using the Adam optimizer and experienced no overfitting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge