Scalable Quantum-Inspired Optimization through Dynamic Qubit Compression

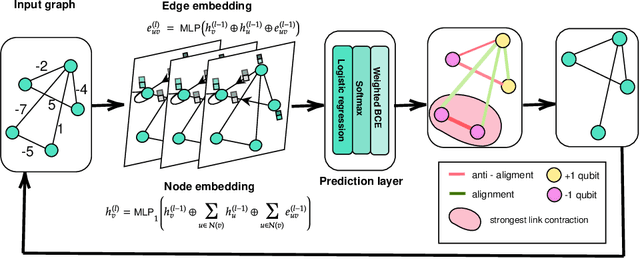
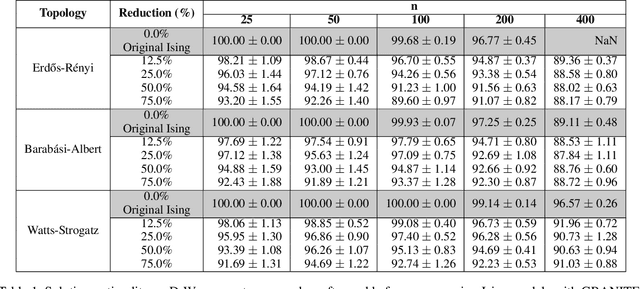
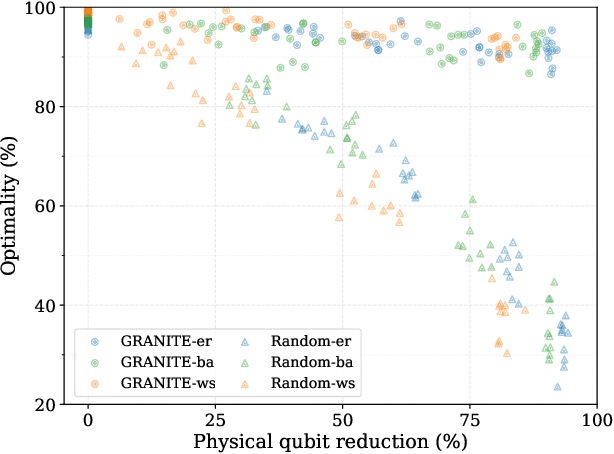
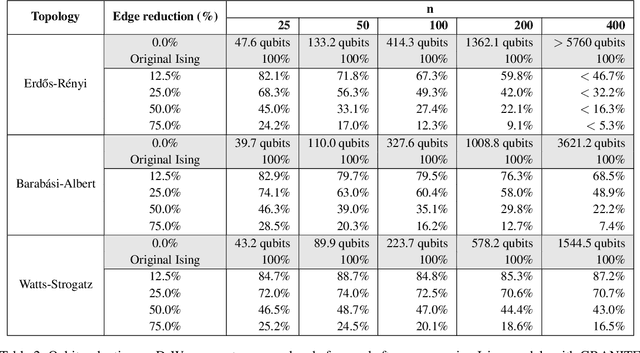
Hard combinatorial optimization problems, often mapped to Ising models, promise potential solutions with quantum advantage but are constrained by limited qubit counts in near-term devices. We present an innovative quantum-inspired framework that dynamically compresses large Ising models to fit available quantum hardware of different sizes. Thus, we aim to bridge the gap between large-scale optimization and current hardware capabilities. Our method leverages a physics-inspired GNN architecture to capture complex interactions in Ising models and accurately predict alignments among neighboring spins (aka qubits) at ground states. By progressively merging such aligned spins, we can reduce the model size while preserving the underlying optimization structure. It also provides a natural trade-off between the solution quality and size reduction, meeting different hardware constraints of quantum computing devices. Extensive numerical studies on Ising instances of diverse topologies show that our method can reduce instance size at multiple levels with virtually no losses in solution quality on the latest D-wave quantum annealers.

Covariant Compositional Networks For Learning Graphs

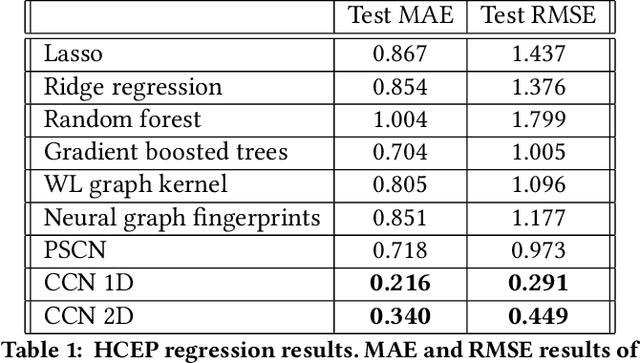
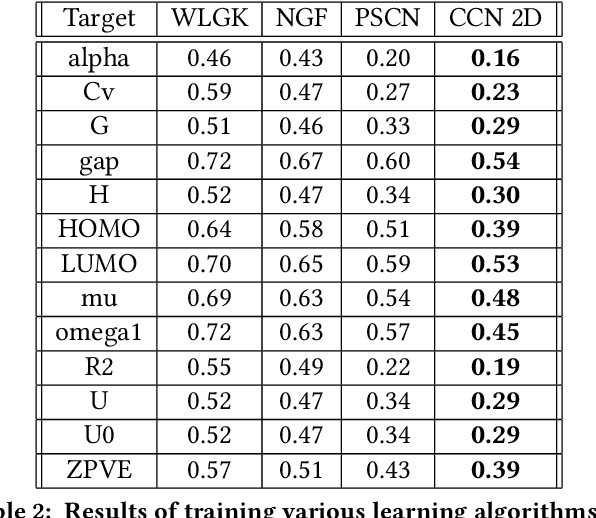
Most existing neural networks for learning graphs address permutation invariance by conceiving of the network as a message passing scheme, where each node sums the feature vectors coming from its neighbors. We argue that this imposes a limitation on their representation power, and instead propose a new general architecture for representing objects consisting of a hierarchy of parts, which we call Covariant Compositional Networks (CCNs). Here, covariance means that the activation of each neuron must transform in a specific way under permutations, similarly to steerability in CNNs. We achieve covariance by making each activation transform according to a tensor representation of the permutation group, and derive the corresponding tensor aggregation rules that each neuron must implement. Experiments show that CCNs can outperform competing methods on standard graph learning benchmarks.