Horace Pan
Covariant Compositional Networks For Learning Graphs
Jan 07, 2018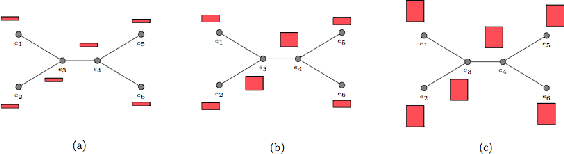
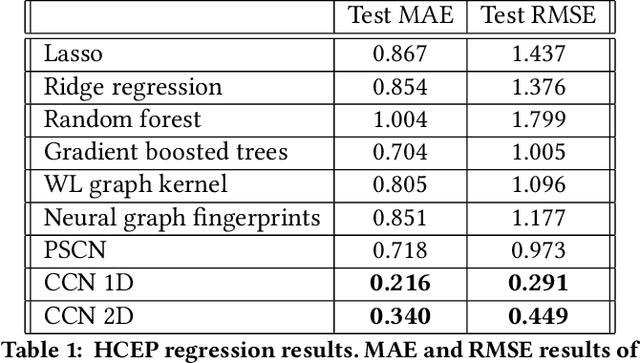
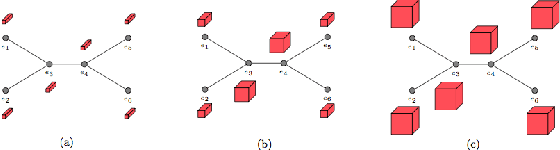
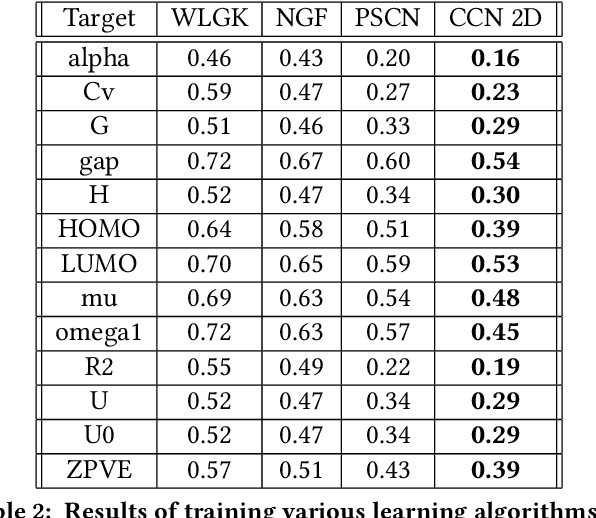
Abstract:Most existing neural networks for learning graphs address permutation invariance by conceiving of the network as a message passing scheme, where each node sums the feature vectors coming from its neighbors. We argue that this imposes a limitation on their representation power, and instead propose a new general architecture for representing objects consisting of a hierarchy of parts, which we call Covariant Compositional Networks (CCNs). Here, covariance means that the activation of each neuron must transform in a specific way under permutations, similarly to steerability in CNNs. We achieve covariance by making each activation transform according to a tensor representation of the permutation group, and derive the corresponding tensor aggregation rules that each neuron must implement. Experiments show that CCNs can outperform competing methods on standard graph learning benchmarks.
The Multiscale Laplacian Graph Kernel
May 30, 2016
Abstract:Many real world graphs, such as the graphs of molecules, exhibit structure at multiple different scales, but most existing kernels between graphs are either purely local or purely global in character. In contrast, by building a hierarchy of nested subgraphs, the Multiscale Laplacian Graph kernels (MLG kernels) that we define in this paper can account for structure at a range of different scales. At the heart of the MLG construction is another new graph kernel, called the Feature Space Laplacian Graph kernel (FLG kernel), which has the property that it can lift a base kernel defined on the vertices of two graphs to a kernel between the graphs. The MLG kernel applies such FLG kernels to subgraphs recursively. To make the MLG kernel computationally feasible, we also introduce a randomized projection procedure, similar to the Nystr\"om method, but for RKHS operators.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge