Graph Neural Controlled Differential Equations for Traffic Forecasting

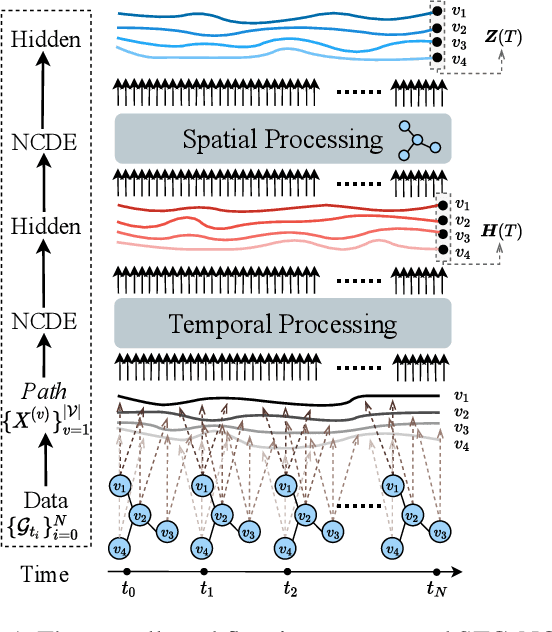
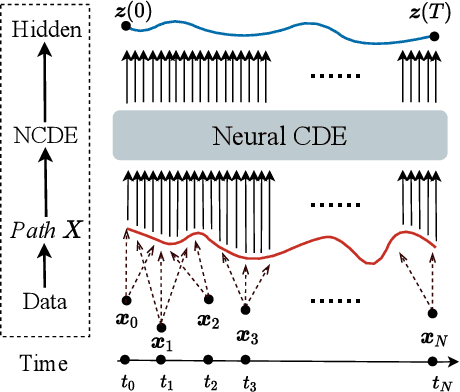
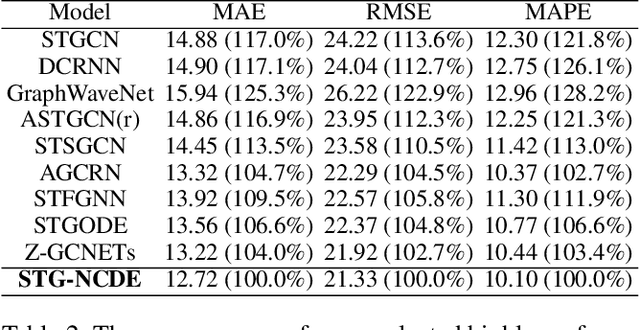
Traffic forecasting is one of the most popular spatio-temporal tasks in the field of machine learning. A prevalent approach in the field is to combine graph convolutional networks and recurrent neural networks for the spatio-temporal processing. There has been fierce competition and many novel methods have been proposed. In this paper, we present the method of spatio-temporal graph neural controlled differential equation (STG-NCDE). Neural controlled differential equations (NCDEs) are a breakthrough concept for processing sequential data. We extend the concept and design two NCDEs: one for the temporal processing and the other for the spatial processing. After that, we combine them into a single framework. We conduct experiments with 6 benchmark datasets and 20 baselines. STG-NCDE shows the best accuracy in all cases, outperforming all those 20 baselines by non-trivial margins.

Climate Modeling with Neural Diffusion Equations

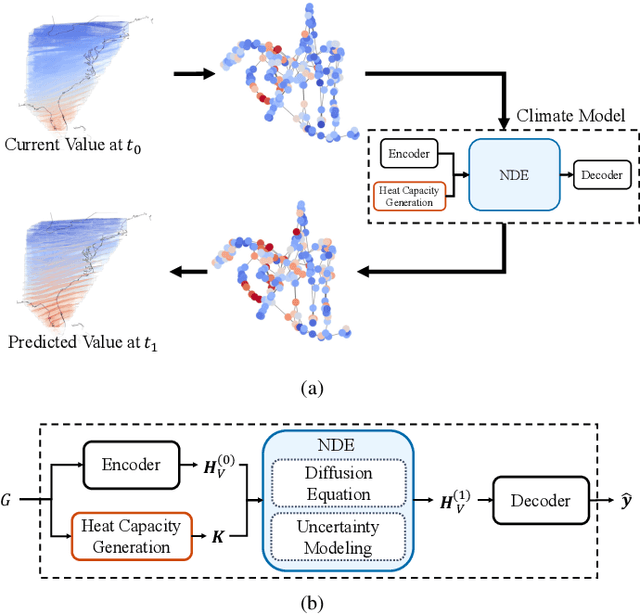
Owing to the remarkable development of deep learning technology, there have been a series of efforts to build deep learning-based climate models. Whereas most of them utilize recurrent neural networks and/or graph neural networks, we design a novel climate model based on the two concepts, the neural ordinary differential equation (NODE) and the diffusion equation. Many physical processes involving a Brownian motion of particles can be described by the diffusion equation and as a result, it is widely used for modeling climate. On the other hand, neural ordinary differential equations (NODEs) are to learn a latent governing equation of ODE from data. In our presented method, we combine them into a single framework and propose a concept, called neural diffusion equation (NDE). Our NDE, equipped with the diffusion equation and one more additional neural network to model inherent uncertainty, can learn an appropriate latent governing equation that best describes a given climate dataset. In our experiments with two real-world and one synthetic datasets and eleven baselines, our method consistently outperforms existing baselines by non-trivial margins.