Implicit factorized transformer approach to fast prediction of turbulent channel flows

Transformer neural operators have recently become an effective approach for surrogate modeling of nonlinear systems governed by partial differential equations (PDEs). In this paper, we introduce a modified implicit factorized transformer (IFactFormer-m) model which replaces the original chained factorized attention with parallel factorized attention. The IFactFormer-m model successfully performs long-term predictions for turbulent channel flow, whereas the original IFactFormer (IFactFormer-o), Fourier neural operator (FNO), and implicit Fourier neural operator (IFNO) exhibit a poor performance. Turbulent channel flows are simulated by direct numerical simulation using fine grids at friction Reynolds numbers $\text{Re}_{\tau}\approx 180,395,590$, and filtered to coarse grids for training neural operator. The neural operator takes the current flow field as input and predicts the flow field at the next time step, and long-term prediction is achieved in the posterior through an autoregressive approach. The prediction results show that IFactFormer-m, compared to other neural operators and the traditional large eddy simulation (LES) methods including dynamic Smagorinsky model (DSM) and the wall-adapted local eddy-viscosity (WALE) model, reduces prediction errors in the short term, and achieves stable and accurate long-term prediction of various statistical properties and flow structures, including the energy spectrum, mean streamwise velocity, root mean square (rms) values of fluctuating velocities, Reynolds shear stress, and spatial structures of instantaneous velocity. Moreover, the trained IFactFormer-m is much faster than traditional LES methods.

Parameter Identification for Partial Differential Equations with Spatiotemporal Varying Coefficients

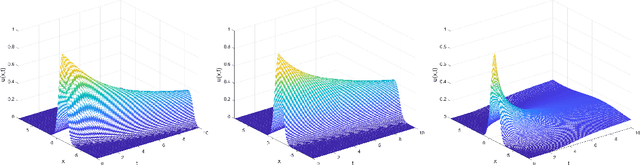
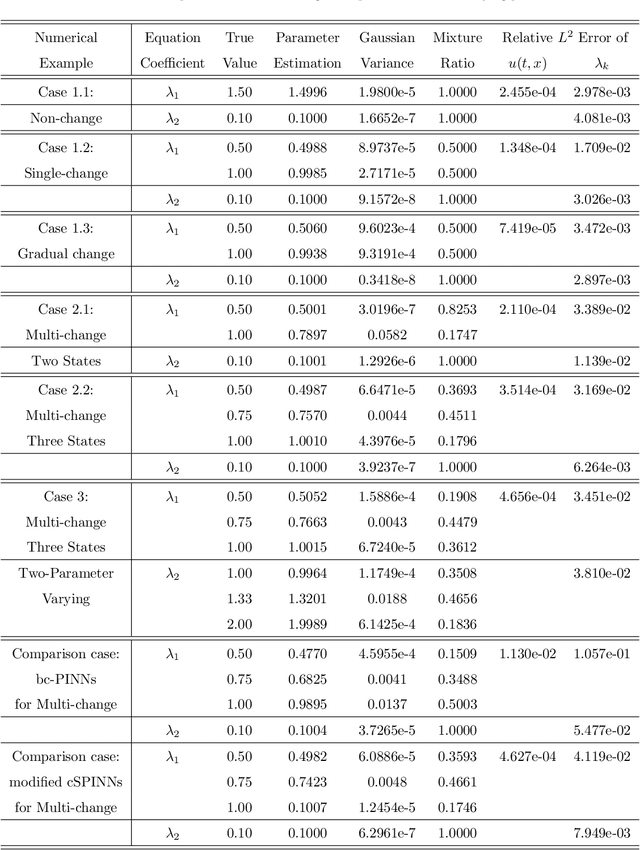
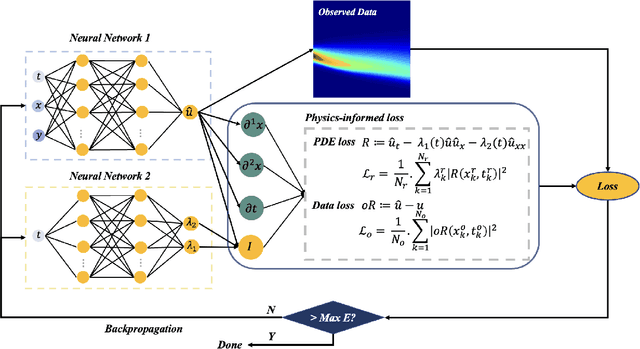
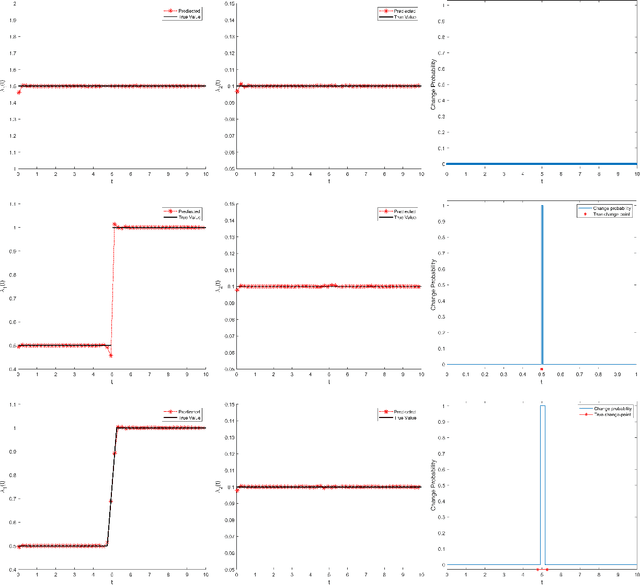
To comprehend complex systems with multiple states, it is imperative to reveal the identity of these states by system outputs. Nevertheless, the mathematical models describing these systems often exhibit nonlinearity so that render the resolution of the parameter inverse problem from the observed spatiotemporal data a challenging endeavor. Starting from the observed data obtained from such systems, we propose a novel framework that facilitates the investigation of parameter identification for multi-state systems governed by spatiotemporal varying parametric partial differential equations. Our framework consists of two integral components: a constrained self-adaptive physics-informed neural network, encompassing a sub-network, as our methodology for parameter identification, and a finite mixture model approach to detect regions of probable parameter variations. Through our scheme, we can precisely ascertain the unknown varying parameters of the complex multi-state system, thereby accomplishing the inversion of the varying parameters. Furthermore, we have showcased the efficacy of our framework on two numerical cases: the 1D Burgers' equation with time-varying parameters and the 2D wave equation with a space-varying parameter.

Automatic Depression Detection: An Emotional Audio-Textual Corpus and a GRU/BiLSTM-based Model

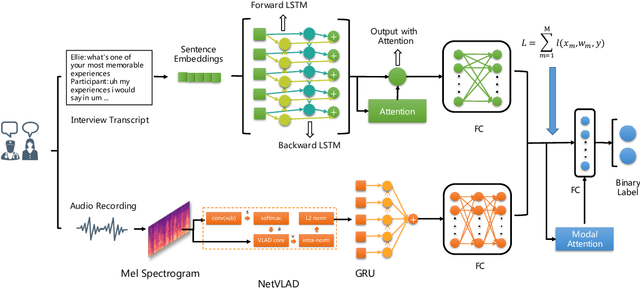
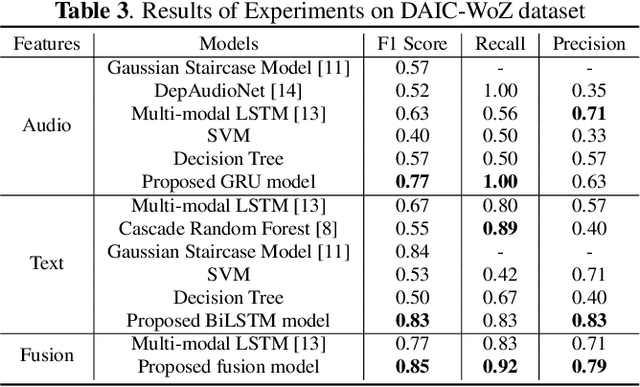
Depression is a global mental health problem, the worst case of which can lead to suicide. An automatic depression detection system provides great help in facilitating depression self-assessment and improving diagnostic accuracy. In this work, we propose a novel depression detection approach utilizing speech characteristics and linguistic contents from participants' interviews. In addition, we establish an Emotional Audio-Textual Depression Corpus (EATD-Corpus) which contains audios and extracted transcripts of responses from depressed and non-depressed volunteers. To the best of our knowledge, EATD-Corpus is the first and only public depression dataset that contains audio and text data in Chinese. Evaluated on two depression datasets, the proposed method achieves the state-of-the-art performances. The outperforming results demonstrate the effectiveness and generalization ability of the proposed method. The source code and EATD-Corpus are available at https://github.com/speechandlanguageprocessing/ICASSP2022-Depression.