Implicit factorized transformer approach to fast prediction of turbulent channel flows

Transformer neural operators have recently become an effective approach for surrogate modeling of nonlinear systems governed by partial differential equations (PDEs). In this paper, we introduce a modified implicit factorized transformer (IFactFormer-m) model which replaces the original chained factorized attention with parallel factorized attention. The IFactFormer-m model successfully performs long-term predictions for turbulent channel flow, whereas the original IFactFormer (IFactFormer-o), Fourier neural operator (FNO), and implicit Fourier neural operator (IFNO) exhibit a poor performance. Turbulent channel flows are simulated by direct numerical simulation using fine grids at friction Reynolds numbers $\text{Re}_{\tau}\approx 180,395,590$, and filtered to coarse grids for training neural operator. The neural operator takes the current flow field as input and predicts the flow field at the next time step, and long-term prediction is achieved in the posterior through an autoregressive approach. The prediction results show that IFactFormer-m, compared to other neural operators and the traditional large eddy simulation (LES) methods including dynamic Smagorinsky model (DSM) and the wall-adapted local eddy-viscosity (WALE) model, reduces prediction errors in the short term, and achieves stable and accurate long-term prediction of various statistical properties and flow structures, including the energy spectrum, mean streamwise velocity, root mean square (rms) values of fluctuating velocities, Reynolds shear stress, and spatial structures of instantaneous velocity. Moreover, the trained IFactFormer-m is much faster than traditional LES methods.

Fourier neural operator for real-time simulation of 3D dynamic urban microclimate

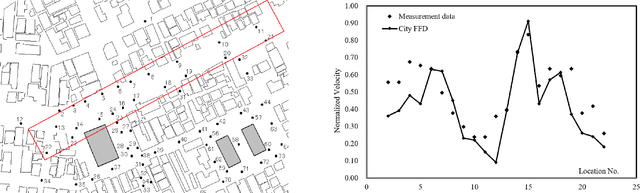
Global urbanization has underscored the significance of urban microclimates for human comfort, health, and building/urban energy efficiency. They profoundly influence building design and urban planning as major environmental impacts. Understanding local microclimates is essential for cities to prepare for climate change and effectively implement resilience measures. However, analyzing urban microclimates requires considering a complex array of outdoor parameters within computational domains at the city scale over a longer period than indoors. As a result, numerical methods like Computational Fluid Dynamics (CFD) become computationally expensive when evaluating the impact of urban microclimates. The rise of deep learning techniques has opened new opportunities for accelerating the modeling of complex non-linear interactions and system dynamics. Recently, the Fourier Neural Operator (FNO) has been shown to be very promising in accelerating solving the Partial Differential Equations (PDEs) and modeling fluid dynamic systems. In this work, we apply the FNO network for real-time three-dimensional (3D) urban wind field simulation. The training and testing data are generated from CFD simulation of the urban area, based on the semi-Lagrangian approach and fractional stepping method to simulate urban microclimate features for modeling large-scale urban problems. Numerical experiments show that the FNO model can accurately reconstruct the instantaneous spatial velocity field. We further evaluate the trained FNO model on unseen data with different wind directions, and the results show that the FNO model can generalize well on different wind directions. More importantly, the FNO approach can make predictions within milliseconds on the graphics processing unit, making real-time simulation of 3D dynamic urban microclimate possible.

Model Reduction with Memory and the Machine Learning of Dynamical Systems

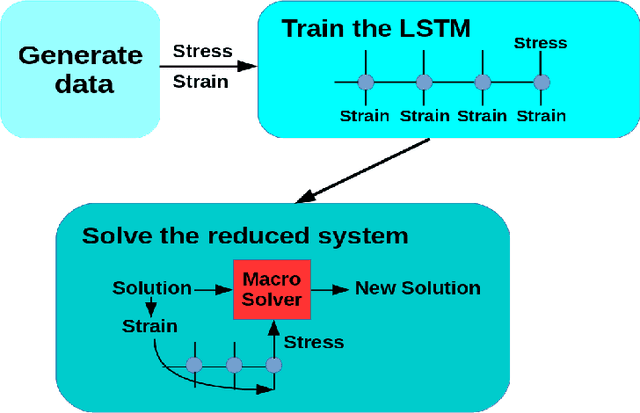
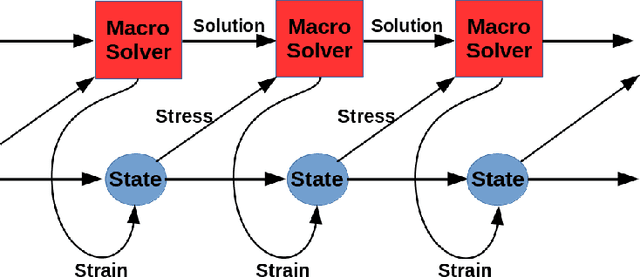
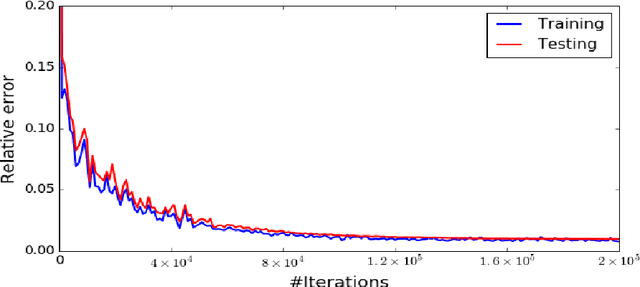
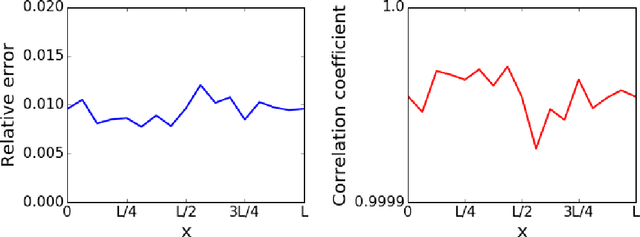
The well-known Mori-Zwanzig theory tells us that model reduction leads to memory effect. For a long time, modeling the memory effect accurately and efficiently has been an important but nearly impossible task in developing a good reduced model. In this work, we explore a natural analogy between recurrent neural networks and the Mori-Zwanzig formalism to establish a systematic approach for developing reduced models with memory. Two training models-a direct training model and a dynamically coupled training model-are proposed and compared. We apply these methods to the Kuramoto-Sivashinsky equation and the Navier-Stokes equation. Numerical experiments show that the proposed method can produce reduced model with good performance on both short-term prediction and long-term statistical properties.