Information Scrambling in Quantum Neural Networks

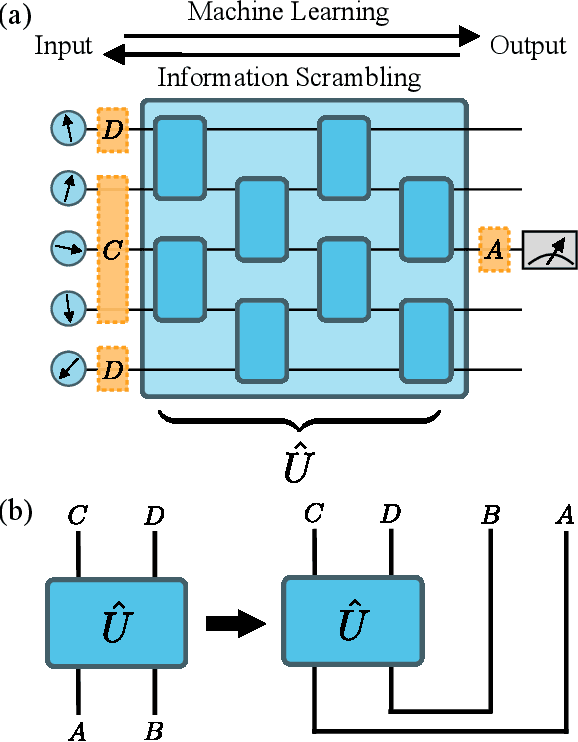
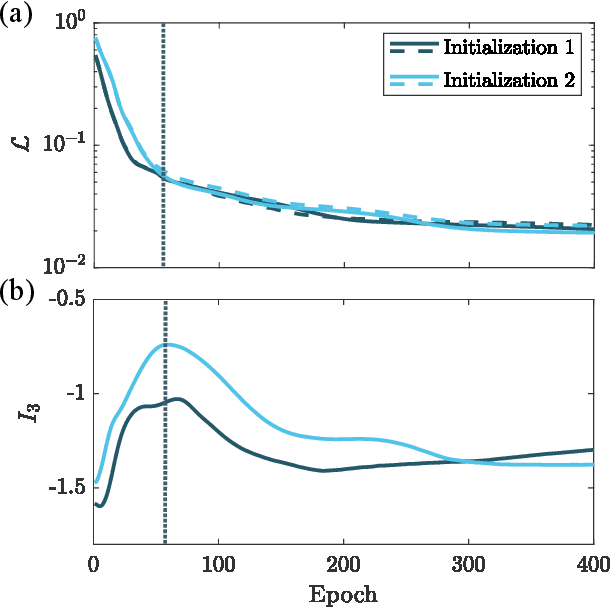
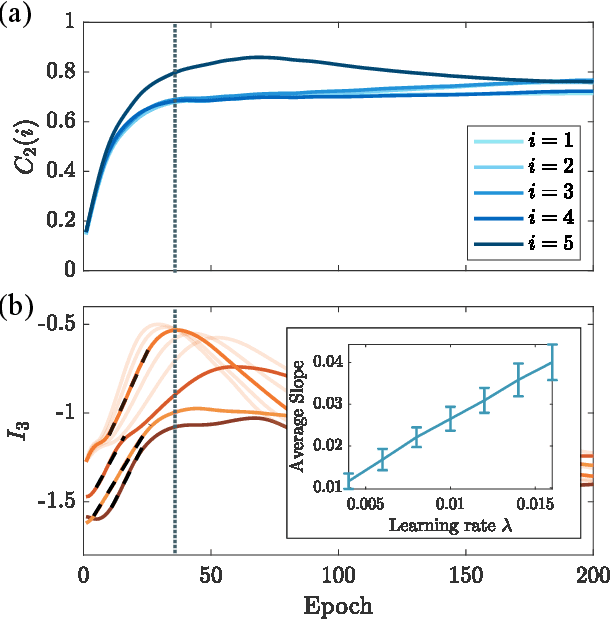
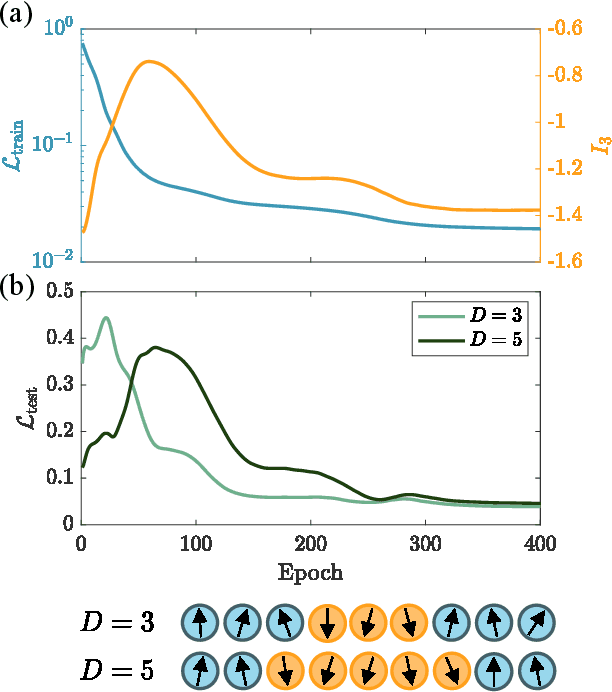
Quantum neural networks are one of the promising applications for near-term noisy intermediate-scale quantum computers. A quantum neural network distills the information from the input wavefunction into the output qubits. In this Letter, we show that this process can also be viewed from the opposite direction: the quantum information in the output qubits is scrambled into the input. This observation motivates us to use the tripartite information, a quantity recently developed to characterize information scrambling, to diagnose the training dynamics of quantum neural networks. We empirically find strong correlation between the dynamical behavior of the tripartite information and the loss function in the training process, from which we identify that the training process has two stages for randomly initialized networks. In the early stage, the network performance improves rapidly and the tripartite information increases linearly with a universal slope, meaning that the neural network becomes less scrambled than the random unitary. In the latter stage, the network performance improves slowly while the tripartite information decreases. We present evidences that the network constructs local correlations in the early stage and learns large-scale structures in the latter stage. We believe this two-stage training dynamics is universal and is applicable to a wide range of problems. Our work builds bridges between two research subjects of quantum neural networks and information scrambling, which opens up a new perspective to understand quantum neural networks.

Mutual Information Scaling and Expressive Power of Sequence Models

Sequence models assign probabilities to variable-length sequences such as natural language texts. The ability of sequence models to capture temporal dependence can be characterized by the temporal scaling of correlation and mutual information. In this paper, we study the mutual information of recurrent neural networks (RNNs) including long short-term memories and self-attention networks such as Transformers. Through a combination of theoretical study of linear RNNs and empirical study of nonlinear RNNs, we find their mutual information decays exponentially in temporal distance. On the other hand, Transformers can capture long-range mutual information more efficiently, making them preferable in modeling sequences with slow power-law mutual information, such as natural languages and stock prices. We discuss the connection of these results with statistical mechanics. We also point out the non-uniformity problem in many natural language datasets. We hope this work provides a new perspective in understanding the expressive power of sequence models and shed new light on improving the architecture of them.

Deep Learning Topological Invariants of Band Insulators

In this work we design and train deep neural networks to predict topological invariants for one-dimensional four-band insulators in AIII class whose topological invariant is the winding number, and two-dimensional two-band insulators in A class whose topological invariant is the Chern number. Given Hamiltonians in the momentum space as the input, neural networks can predict topological invariants for both classes with accuracy close to or higher than 90%, even for Hamiltonians whose invariants are beyond the training data set. Despite the complexity of the neural network, we find that the output of certain intermediate hidden layers resembles either the winding angle for models in AIII class or the solid angle (Berry curvature) for models in A class, indicating that neural networks essentially capture the mathematical formula of topological invariants. Our work demonstrates the ability of neural networks to predict topological invariants for complicated models with local Hamiltonians as the only input, and offers an example that even a deep neural network is understandable.

Visualizing Neural Network Developing Perturbation Theory

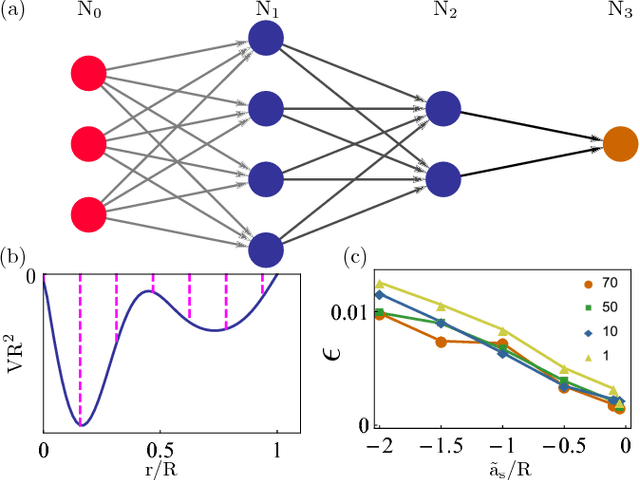
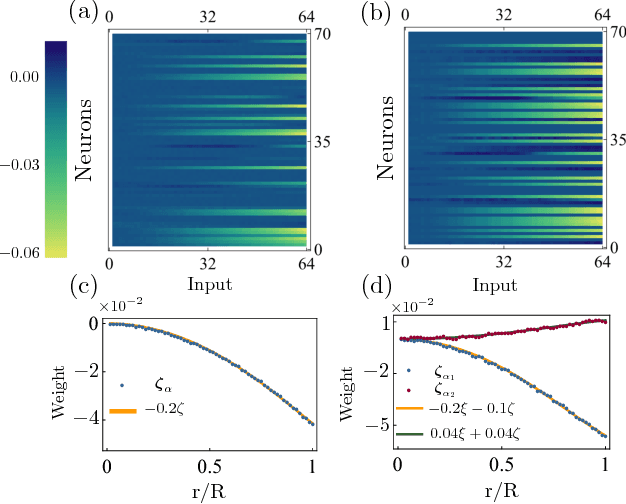
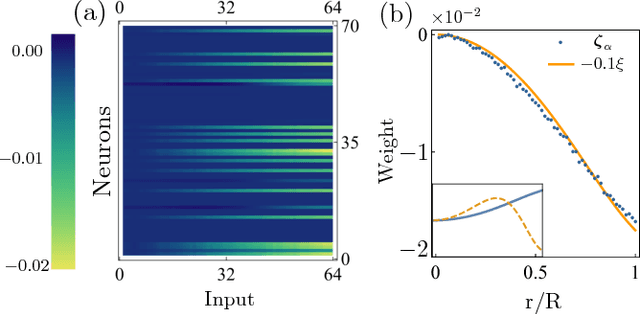
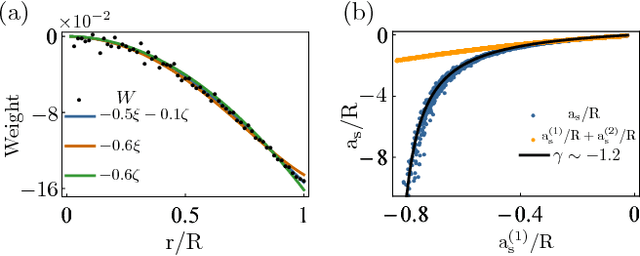
In this letter, motivated by the question that whether the empirical fitting of data by neural network can yield the same structure of physical laws, we apply the neural network to a simple quantum mechanical two-body scattering problem with short-range potentials, which by itself also plays an important role in many branches of physics. We train a neural network to accurately predict $ s $-wave scattering length, which governs the low-energy scattering physics, directly from the scattering potential without solving Schr\"odinger equation or obtaining the wavefunction. After analyzing the neural network, it is shown that the neural network develops perturbation theory order by order when the potential increases. This provides an important benchmark to the machine-assisted physics research or even automated machine learning physics laws.

Machine Learning Topological Invariants with Neural Networks

In this Letter we supervisedly train neural networks to distinguish different topological phases in the context of topological band insulators. After training with Hamiltonians of one-dimensional insulators with chiral symmetry, the neural network can predict their topological winding numbers with nearly 100% accuracy, even for Hamiltonians with larger winding numbers that are not included in the training data. These results show a remarkable success that the neural network can capture the global and nonlinear topological features of quantum phases from local inputs. By opening up the neural network, we confirm that the network does learn the discrete version of the winding number formula. We also make a couple of remarks regarding the role of the symmetry and the opposite effect of regularization techniques when applying machine learning to physical systems.