Information Scrambling in Quantum Neural Networks

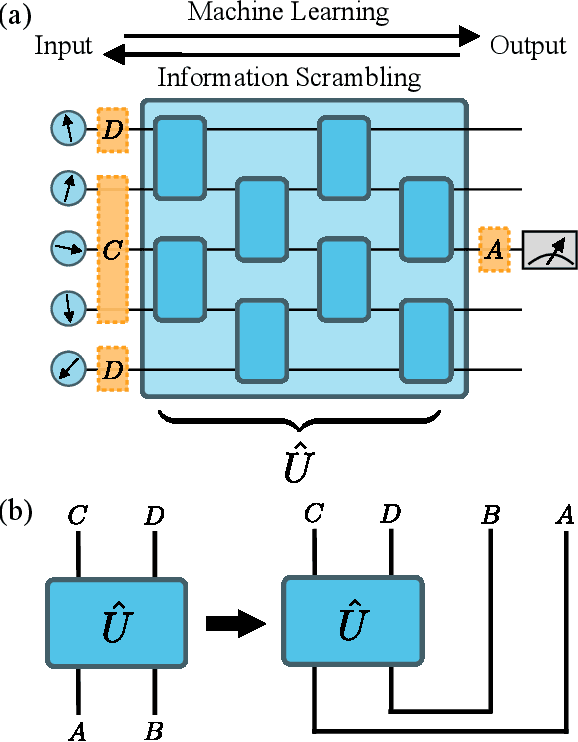
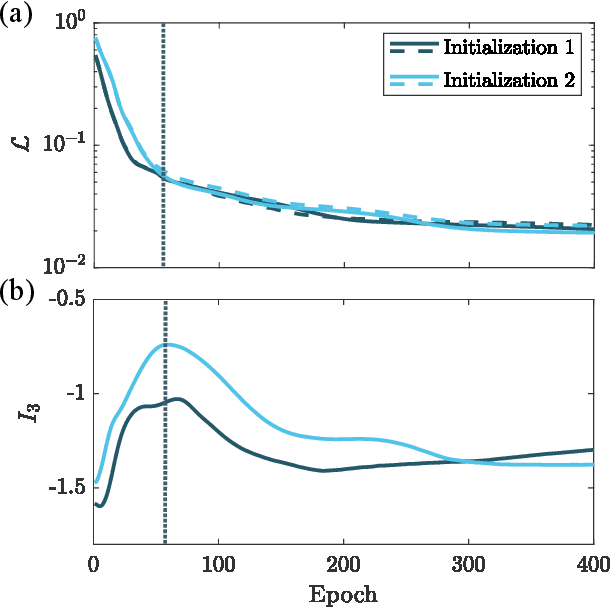
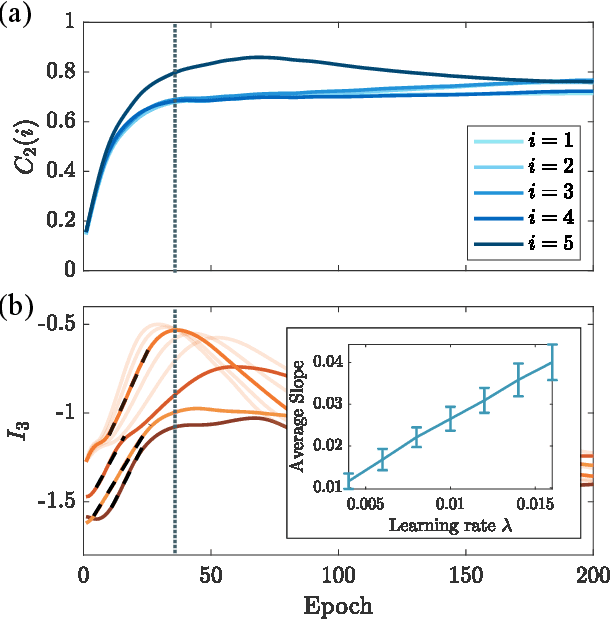
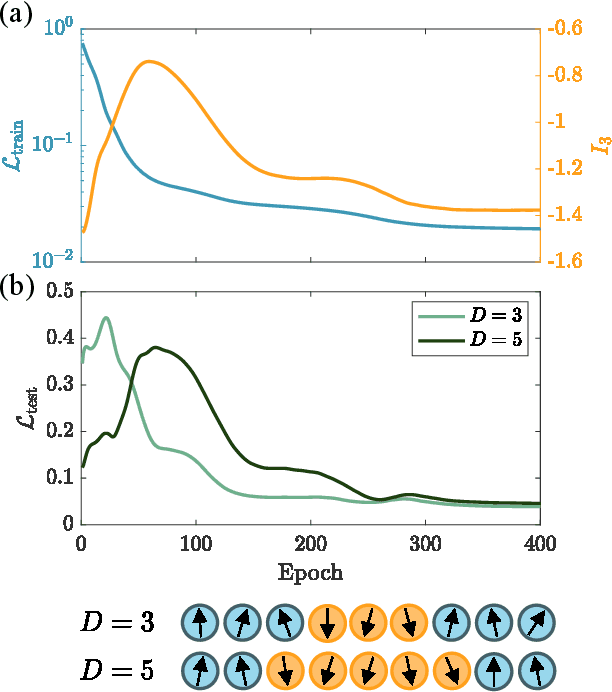
Quantum neural networks are one of the promising applications for near-term noisy intermediate-scale quantum computers. A quantum neural network distills the information from the input wavefunction into the output qubits. In this Letter, we show that this process can also be viewed from the opposite direction: the quantum information in the output qubits is scrambled into the input. This observation motivates us to use the tripartite information, a quantity recently developed to characterize information scrambling, to diagnose the training dynamics of quantum neural networks. We empirically find strong correlation between the dynamical behavior of the tripartite information and the loss function in the training process, from which we identify that the training process has two stages for randomly initialized networks. In the early stage, the network performance improves rapidly and the tripartite information increases linearly with a universal slope, meaning that the neural network becomes less scrambled than the random unitary. In the latter stage, the network performance improves slowly while the tripartite information decreases. We present evidences that the network constructs local correlations in the early stage and learns large-scale structures in the latter stage. We believe this two-stage training dynamics is universal and is applicable to a wide range of problems. Our work builds bridges between two research subjects of quantum neural networks and information scrambling, which opens up a new perspective to understand quantum neural networks.