A Statistical Decision-Theoretic Framework for Social Choice

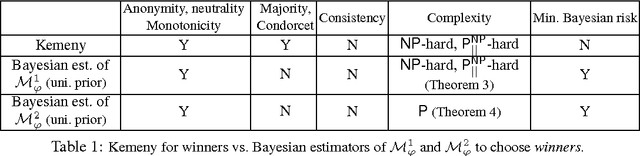
In this paper, we take a statistical decision-theoretic viewpoint on social choice, putting a focus on the decision to be made on behalf of a system of agents. In our framework, we are given a statistical ranking model, a decision space, and a loss function defined on (parameter, decision) pairs, and formulate social choice mechanisms as decision rules that minimize expected loss. This suggests a general framework for the design and analysis of new social choice mechanisms. We compare Bayesian estimators, which minimize Bayesian expected loss, for the Mallows model and the Condorcet model respectively, and the Kemeny rule. We consider various normative properties, in addition to computational complexity and asymptotic behavior. In particular, we show that the Bayesian estimator for the Condorcet model satisfies some desired properties such as anonymity, neutrality, and monotonicity, can be computed in polynomial time, and is asymptotically different from the other two rules when the data are generated from the Condorcet model for some ground truth parameter.

Preference Elicitation For General Random Utility Models

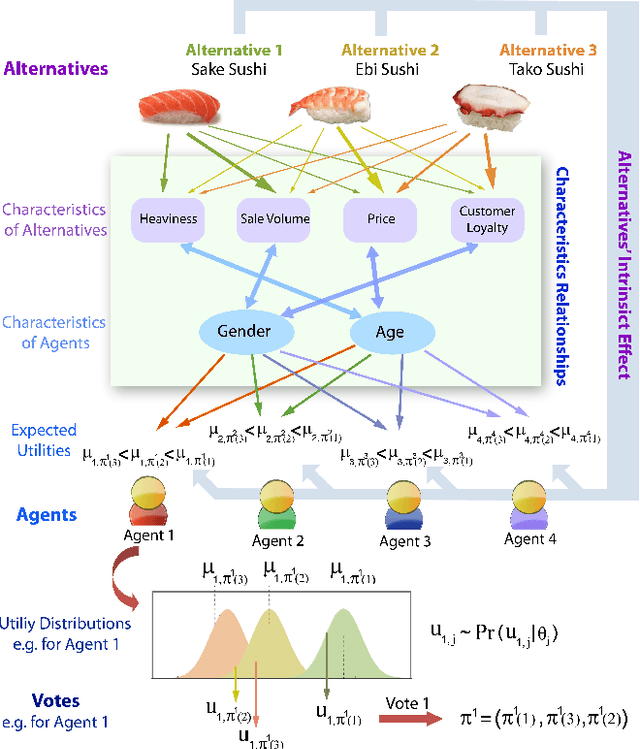
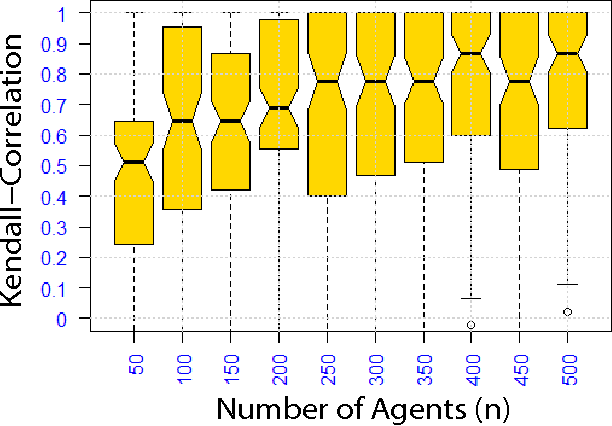
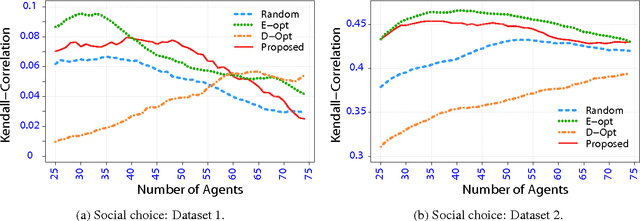
This paper discusses {General Random Utility Models (GRUMs)}. These are a class of parametric models that generate partial ranks over alternatives given attributes of agents and alternatives. We propose two preference elicitation scheme for GRUMs developed from principles in Bayesian experimental design, one for social choice and the other for personalized choice. We couple this with a general Monte-Carlo-Expectation-Maximization (MC-EM) based algorithm for MAP inference under GRUMs. We also prove uni-modality of the likelihood functions for a class of GRUMs. We examine the performance of various criteria by experimental studies, which show that the proposed elicitation scheme increases the precision of estimation.

Random Utility Theory for Social Choice

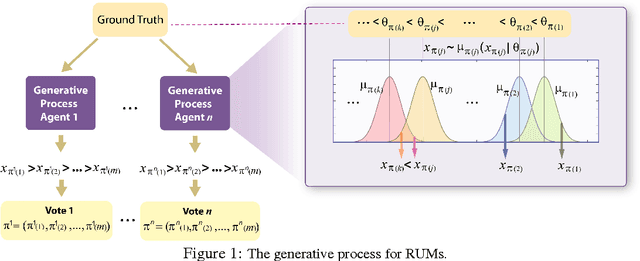
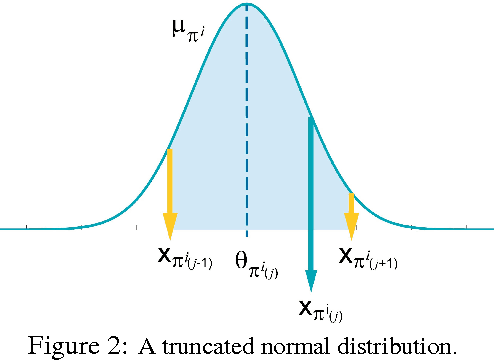
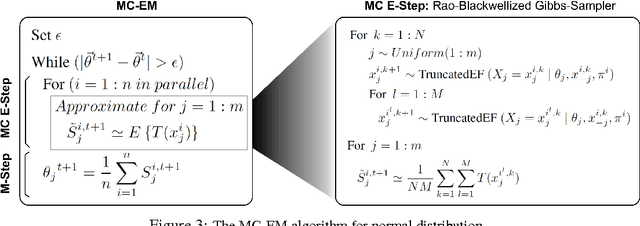
Random utility theory models an agent's preferences on alternatives by drawing a real-valued score on each alternative (typically independently) from a parameterized distribution, and then ranking the alternatives according to scores. A special case that has received significant attention is the Plackett-Luce model, for which fast inference methods for maximum likelihood estimators are available. This paper develops conditions on general random utility models that enable fast inference within a Bayesian framework through MC-EM, providing concave loglikelihood functions and bounded sets of global maxima solutions. Results on both real-world and simulated data provide support for the scalability of the approach and capability for model selection among general random utility models including Plackett-Luce.

Graphlet decomposition of a weighted network

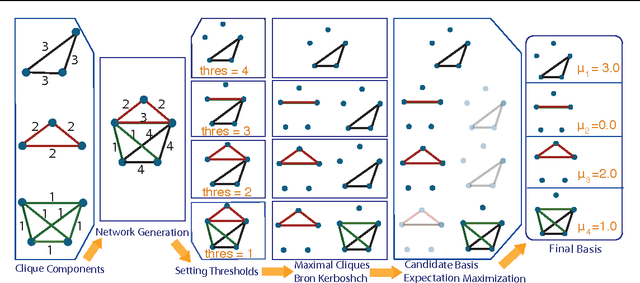
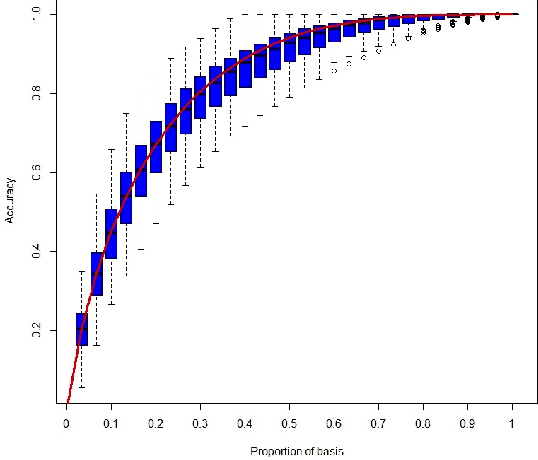
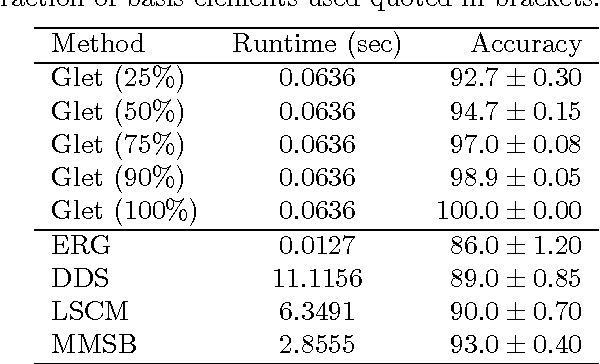
We introduce the graphlet decomposition of a weighted network, which encodes a notion of social information based on social structure. We develop a scalable inference algorithm, which combines EM with Bron-Kerbosch in a novel fashion, for estimating the parameters of the model underlying graphlets using one network sample. We explore some theoretical properties of the graphlet decomposition, including computational complexity, redundancy and expected accuracy. We demonstrate graphlets on synthetic and real data. We analyze messaging patterns on Facebook and criminal associations in the 19th century.