Preference Elicitation For General Random Utility Models

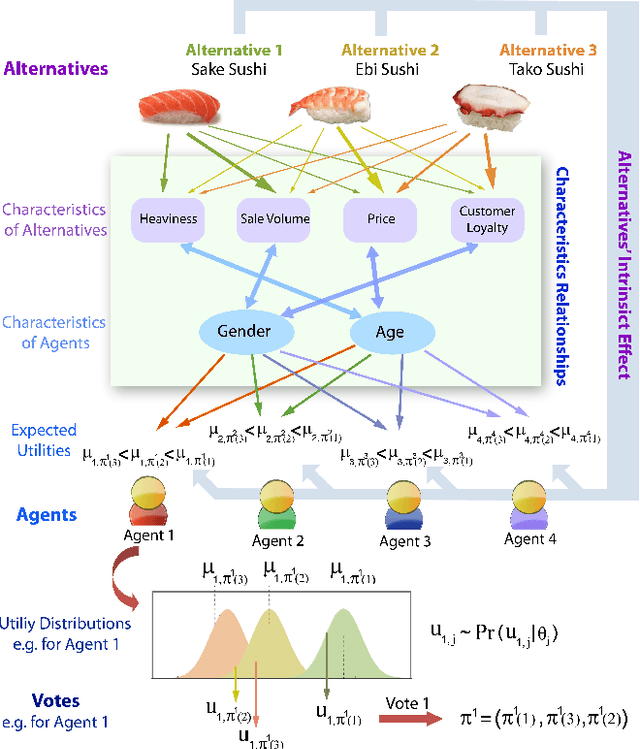
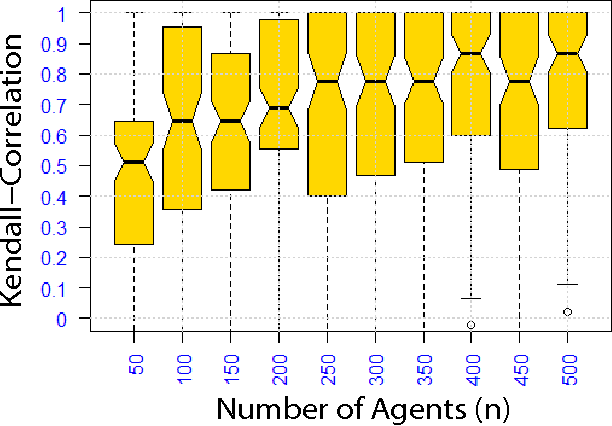
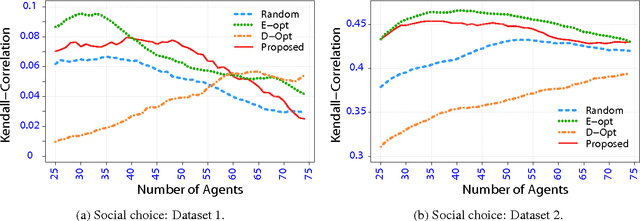
This paper discusses {General Random Utility Models (GRUMs)}. These are a class of parametric models that generate partial ranks over alternatives given attributes of agents and alternatives. We propose two preference elicitation scheme for GRUMs developed from principles in Bayesian experimental design, one for social choice and the other for personalized choice. We couple this with a general Monte-Carlo-Expectation-Maximization (MC-EM) based algorithm for MAP inference under GRUMs. We also prove uni-modality of the likelihood functions for a class of GRUMs. We examine the performance of various criteria by experimental studies, which show that the proposed elicitation scheme increases the precision of estimation.