Random Utility Theory for Social Choice
Paper and Code
Nov 11, 2012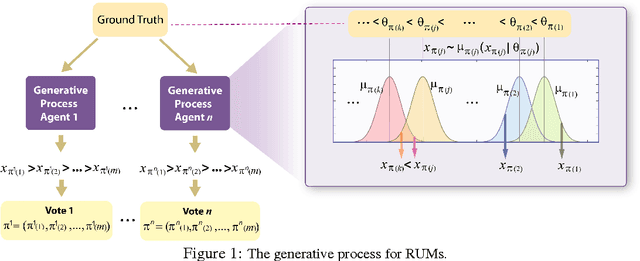

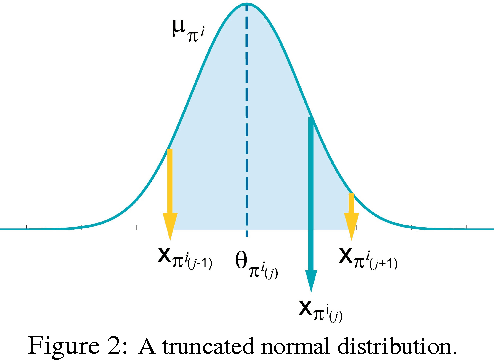
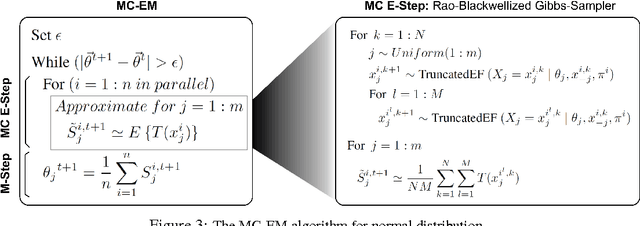
Random utility theory models an agent's preferences on alternatives by drawing a real-valued score on each alternative (typically independently) from a parameterized distribution, and then ranking the alternatives according to scores. A special case that has received significant attention is the Plackett-Luce model, for which fast inference methods for maximum likelihood estimators are available. This paper develops conditions on general random utility models that enable fast inference within a Bayesian framework through MC-EM, providing concave loglikelihood functions and bounded sets of global maxima solutions. Results on both real-world and simulated data provide support for the scalability of the approach and capability for model selection among general random utility models including Plackett-Luce.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge