A Poisson convolution model for characterizing topical content with word frequency and exclusivity

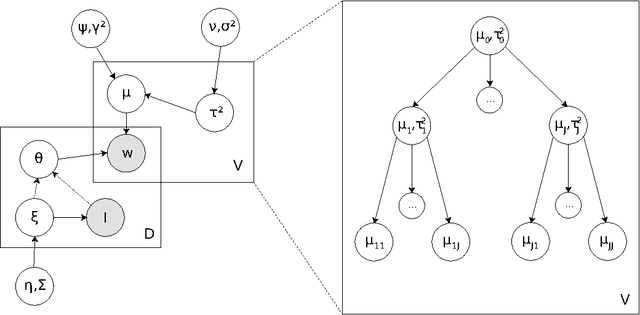
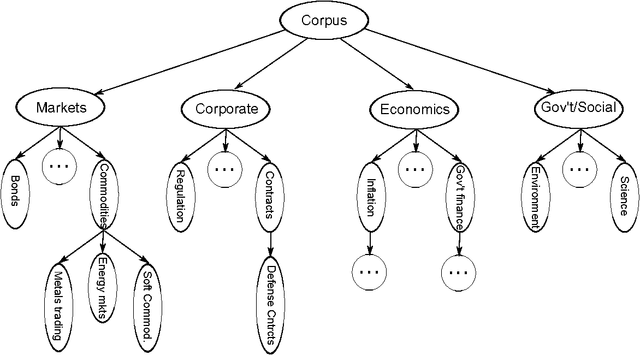
An ongoing challenge in the analysis of document collections is how to summarize content in terms of a set of inferred themes that can be interpreted substantively in terms of topics. The current practice of parametrizing the themes in terms of most frequent words limits interpretability by ignoring the differential use of words across topics. We argue that words that are both common and exclusive to a theme are more effective at characterizing topical content. We consider a setting where professional editors have annotated documents to a collection of topic categories, organized into a tree, in which leaf-nodes correspond to the most specific topics. Each document is annotated to multiple categories, at different levels of the tree. We introduce a hierarchical Poisson convolution model to analyze annotated documents in this setting. The model leverages the structure among categories defined by professional editors to infer a clear semantic description for each topic in terms of words that are both frequent and exclusive. We carry out a large randomized experiment on Amazon Turk to demonstrate that topic summaries based on the FREX score are more interpretable than currently established frequency based summaries, and that the proposed model produces more efficient estimates of exclusivity than with currently models. We also develop a parallelized Hamiltonian Monte Carlo sampler that allows the inference to scale to millions of documents.

Stochastic blockmodel approximation of a graphon: Theory and consistent estimation

Non-parametric approaches for analyzing network data based on exchangeable graph models (ExGM) have recently gained interest. The key object that defines an ExGM is often referred to as a graphon. This non-parametric perspective on network modeling poses challenging questions on how to make inference on the graphon underlying observed network data. In this paper, we propose a computationally efficient procedure to estimate a graphon from a set of observed networks generated from it. This procedure is based on a stochastic blockmodel approximation (SBA) of the graphon. We show that, by approximating the graphon with a stochastic block model, the graphon can be consistently estimated, that is, the estimation error vanishes as the size of the graph approaches infinity.

Graphlet decomposition of a weighted network

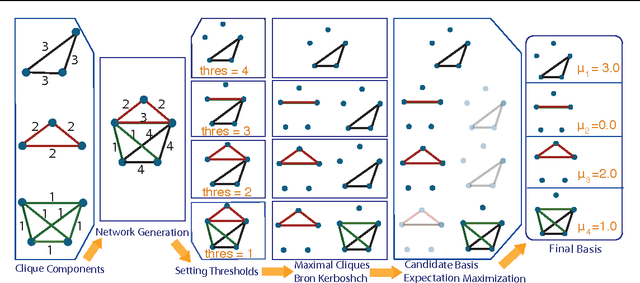
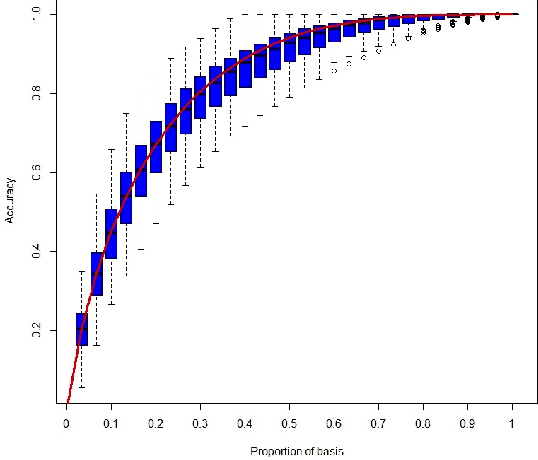
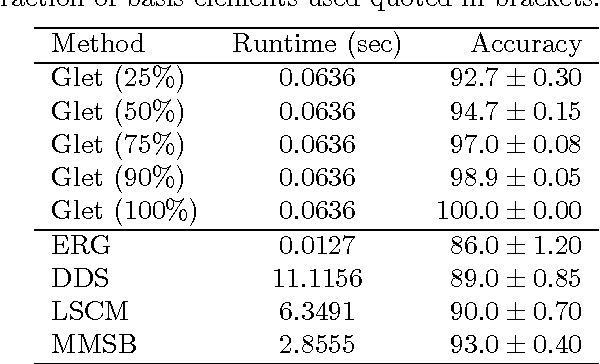
We introduce the graphlet decomposition of a weighted network, which encodes a notion of social information based on social structure. We develop a scalable inference algorithm, which combines EM with Bron-Kerbosch in a novel fashion, for estimating the parameters of the model underlying graphlets using one network sample. We explore some theoretical properties of the graphlet decomposition, including computational complexity, redundancy and expected accuracy. We demonstrate graphlets on synthetic and real data. We analyze messaging patterns on Facebook and criminal associations in the 19th century.

A survey of statistical network models

Networks are ubiquitous in science and have become a focal point for discussion in everyday life. Formal statistical models for the analysis of network data have emerged as a major topic of interest in diverse areas of study, and most of these involve a form of graphical representation. Probability models on graphs date back to 1959. Along with empirical studies in social psychology and sociology from the 1960s, these early works generated an active network community and a substantial literature in the 1970s. This effort moved into the statistical literature in the late 1970s and 1980s, and the past decade has seen a burgeoning network literature in statistical physics and computer science. The growth of the World Wide Web and the emergence of online networking communities such as Facebook, MySpace, and LinkedIn, and a host of more specialized professional network communities has intensified interest in the study of networks and network data. Our goal in this review is to provide the reader with an entry point to this burgeoning literature. We begin with an overview of the historical development of statistical network modeling and then we introduce a number of examples that have been studied in the network literature. Our subsequent discussion focuses on a number of prominent static and dynamic network models and their interconnections. We emphasize formal model descriptions, and pay special attention to the interpretation of parameters and their estimation. We end with a description of some open problems and challenges for machine learning and statistics.

Getting started in probabilistic graphical models

Probabilistic graphical models (PGMs) have become a popular tool for computational analysis of biological data in a variety of domains. But, what exactly are they and how do they work? How can we use PGMs to discover patterns that are biologically relevant? And to what extent can PGMs help us formulate new hypotheses that are testable at the bench? This note sketches out some answers and illustrates the main ideas behind the statistical approach to biological pattern discovery.

Mixed membership stochastic blockmodels

Observations consisting of measurements on relationships for pairs of objects arise in many settings, such as protein interaction and gene regulatory networks, collections of author-recipient email, and social networks. Analyzing such data with probabilisic models can be delicate because the simple exchangeability assumptions underlying many boilerplate models no longer hold. In this paper, we describe a latent variable model of such data called the mixed membership stochastic blockmodel. This model extends blockmodels for relational data to ones which capture mixed membership latent relational structure, thus providing an object-specific low-dimensional representation. We develop a general variational inference algorithm for fast approximate posterior inference. We explore applications to social and protein interaction networks.