SPRINT Enables Interpretable and Ultra-Fast Virtual Screening against Thousands of Proteomes

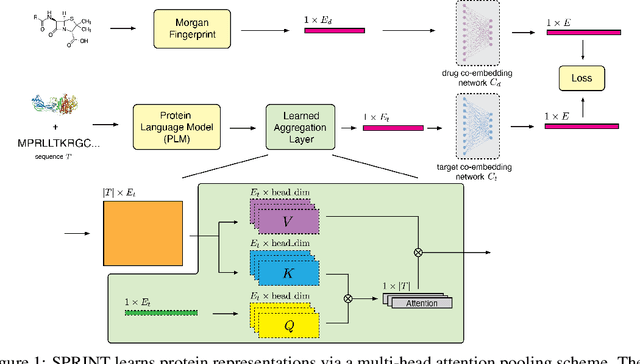
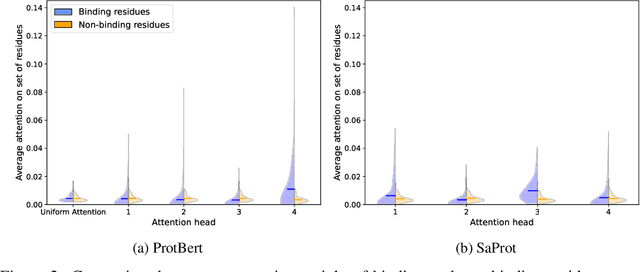
Virtual screening of small molecules against protein targets can accelerate drug discovery and development by predicting drug-target interactions (DTIs). However, structure-based methods like molecular docking are too slow to allow for broad proteome-scale screens, limiting their application in screening for off-target effects or new molecular mechanisms. Recently, vector-based methods using protein language models (PLMs) have emerged as a complementary approach that bypasses explicit 3D structure modeling. Here, we develop SPRINT, a vector-based approach for screening entire chemical libraries against whole proteomes for DTIs and novel mechanisms of action. SPRINT improves on prior work by using a self-attention based architecture and structure-aware PLMs to learn drug-target co-embeddings for binder prediction, search, and retrieval. SPRINT achieves SOTA enrichment factors in virtual screening on LIT-PCBA and DTI classification benchmarks, while providing interpretability in the form of residue-level attention maps. In addition to being both accurate and interpretable, SPRINT is ultra-fast: querying the whole human proteome against the ENAMINE Real Database (6.7B drugs) for the 100 most likely binders per protein takes 16 minutes. SPRINT promises to enable virtual screening at an unprecedented scale, opening up new opportunities for in silico drug repurposing and development. SPRINT is available on the web as ColabScreen: https://bit.ly/colab-screen

Tree-wise Distribution Sensitive hashing: Efficient Maximum likelihood Classification by joint dimensionality reduction in known probabilistic settings

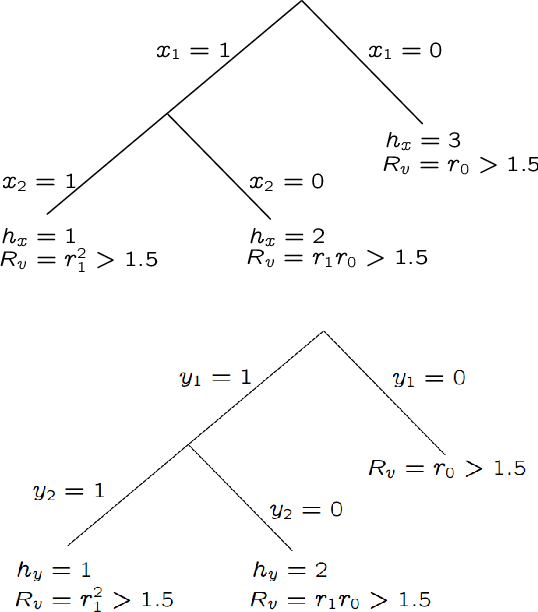
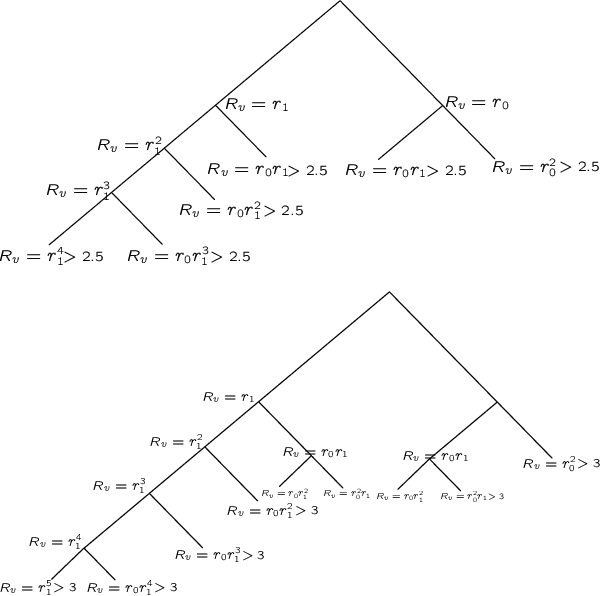
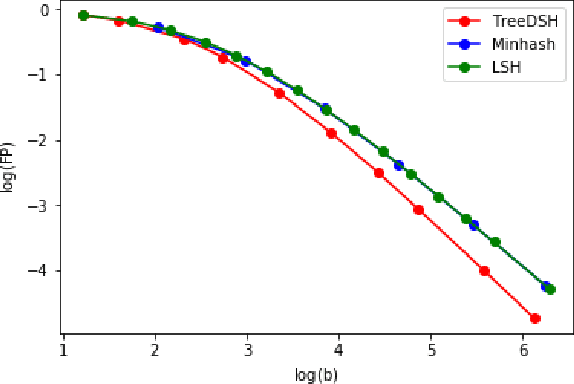
We consider the problem of maximum likelihood classification of a high dimensional data point y to billions of classes $x_1,...,x_N$, where the conditional probability p(y|x) is known. In the most general case, the complexity of the brute-force method for this classification grows linearly, O(N), with the number of classes N. Efficient multiclass classification methods have been introduced to solve this problem with logarithmic complexity. However, these methods suffer from the curse of dimensionality, i.e., in large dimensions their complexity approaches $O(N)$ per query data point. In the special case where the conditional probability distribution $p(y|x)$ is a Gaussian centered at x, i.e., $p(y|x) \propto N (x,\sigma)$, the maximum likelihood classification reduces to the nearest neighbor search with the Euclidean norm. Sublinear methods based on locality sensitive hashing (LSH) have been introduced to solve an approximate version of the nearest neighbor search for high dimensional data. Inspired by these advances, here we introduce distribution sensitive hashing (DSH) to solve an approximate version of the maximum likelihood classification problem through joint dimensionality reduction. In the case of discrete probability distributions, we design TreeDSH, a universal family of distribution sensitive hashes based on the decision trees, and show that their complexity grow sub-linearly. Theory and simulation presented in this paper demonstrate that TreeDSH is more efficient than LSH-hamming and Min-Hashing schemes. Finally, we apply TreeDSH to the problem of peptide identification from mass spectrometry data.