LLMs Are Not Intelligent Thinkers: Introducing Mathematical Topic Tree Benchmark for Comprehensive Evaluation of LLMs

Large language models (LLMs) demonstrate impressive capabilities in mathematical reasoning. However, despite these achievements, current evaluations are mostly limited to specific mathematical topics, and it remains unclear whether LLMs are genuinely engaging in reasoning. To address these gaps, we present the Mathematical Topics Tree (MaTT) benchmark, a challenging and structured benchmark that offers 1,958 questions across a wide array of mathematical subjects, each paired with a detailed hierarchical chain of topics. Upon assessing different LLMs using the MaTT benchmark, we find that the most advanced model, GPT-4, achieved a mere 54\% accuracy in a multiple-choice scenario. Interestingly, even when employing Chain-of-Thought prompting, we observe mostly no notable improvement. Moreover, LLMs accuracy dramatically reduced by up to 24.2 percentage point when the questions were presented without providing choices. Further detailed analysis of the LLMs' performance across a range of topics showed significant discrepancy even for closely related subtopics within the same general mathematical area. In an effort to pinpoint the reasons behind LLMs performances, we conducted a manual evaluation of the completeness and correctness of the explanations generated by GPT-4 when choices were available. Surprisingly, we find that in only 53.3\% of the instances where the model provided a correct answer, the accompanying explanations were deemed complete and accurate, i.e., the model engaged in genuine reasoning.

Tree-wise Distribution Sensitive hashing: Efficient Maximum likelihood Classification by joint dimensionality reduction in known probabilistic settings

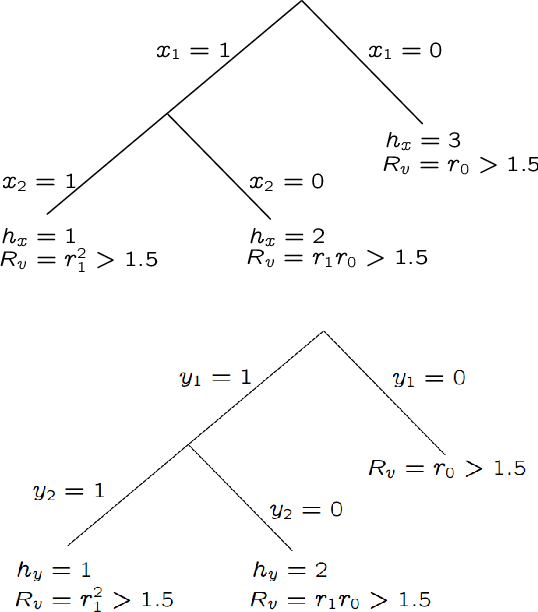
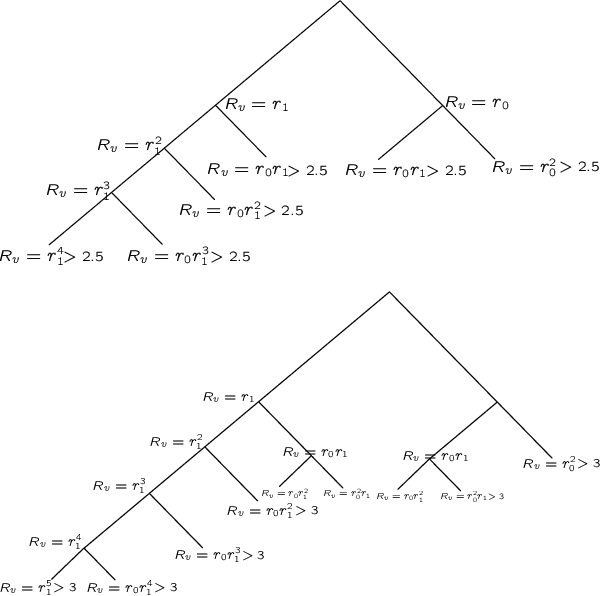
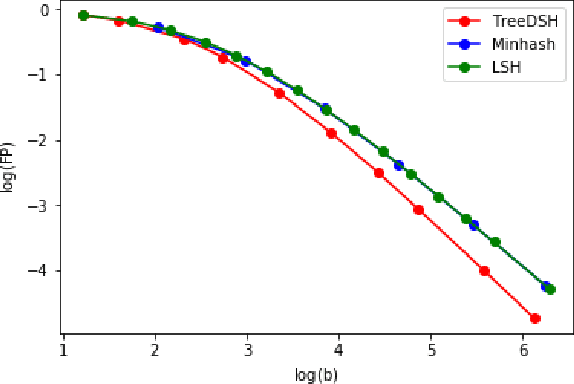
We consider the problem of maximum likelihood classification of a high dimensional data point y to billions of classes $x_1,...,x_N$, where the conditional probability p(y|x) is known. In the most general case, the complexity of the brute-force method for this classification grows linearly, O(N), with the number of classes N. Efficient multiclass classification methods have been introduced to solve this problem with logarithmic complexity. However, these methods suffer from the curse of dimensionality, i.e., in large dimensions their complexity approaches $O(N)$ per query data point. In the special case where the conditional probability distribution $p(y|x)$ is a Gaussian centered at x, i.e., $p(y|x) \propto N (x,\sigma)$, the maximum likelihood classification reduces to the nearest neighbor search with the Euclidean norm. Sublinear methods based on locality sensitive hashing (LSH) have been introduced to solve an approximate version of the nearest neighbor search for high dimensional data. Inspired by these advances, here we introduce distribution sensitive hashing (DSH) to solve an approximate version of the maximum likelihood classification problem through joint dimensionality reduction. In the case of discrete probability distributions, we design TreeDSH, a universal family of distribution sensitive hashes based on the decision trees, and show that their complexity grow sub-linearly. Theory and simulation presented in this paper demonstrate that TreeDSH is more efficient than LSH-hamming and Min-Hashing schemes. Finally, we apply TreeDSH to the problem of peptide identification from mass spectrometry data.