A Computationally Efficient Approach to Non-cooperative Target Detection and Tracking with Almost No A-priori Information

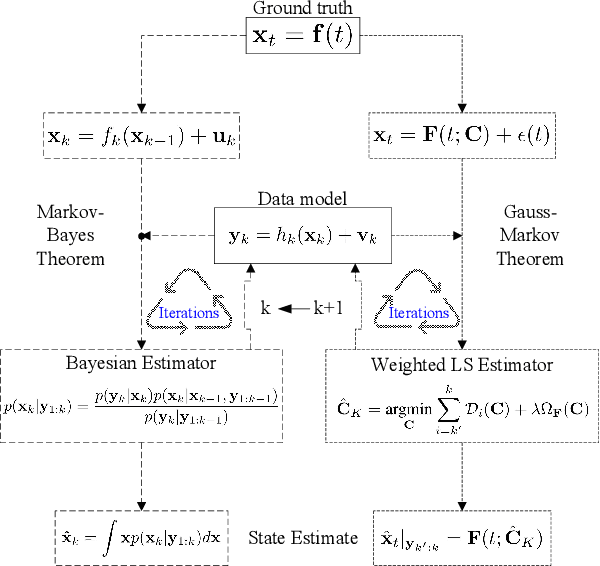
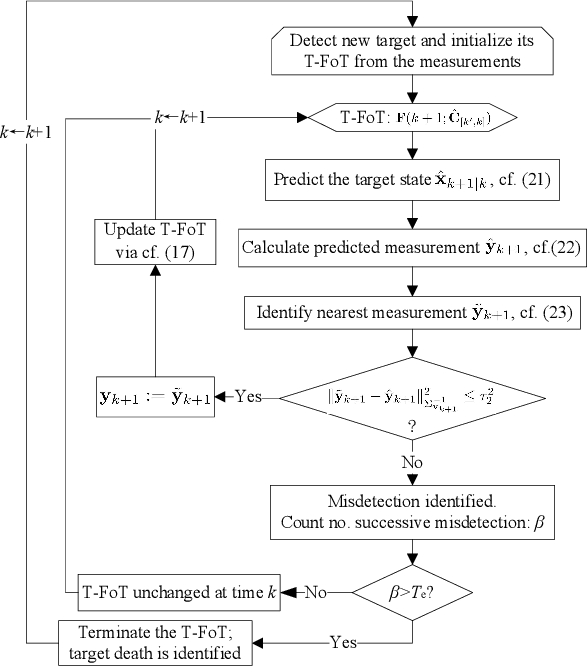
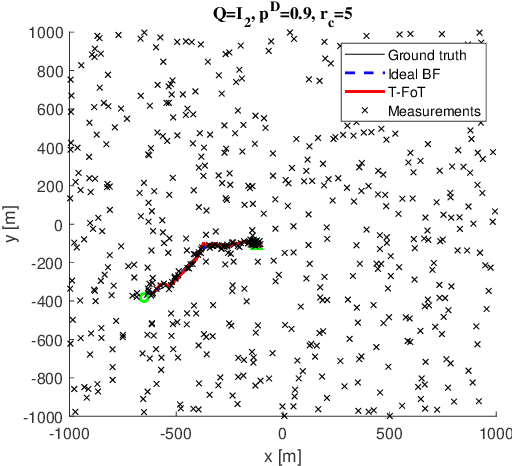
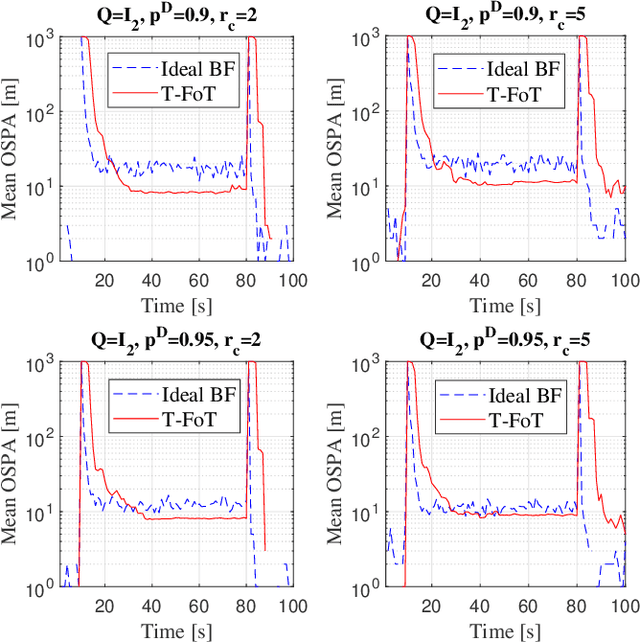
This paper addresses the problem of real-time detection and tracking of a non-cooperative target in the challenging scenario with almost no a-priori information about target birth, death, dynamics and detection probability. Furthermore, there are false and missing data at unknown yet low rates in the measurements. The only information given in advance is about the target-measurement model and the constraint that there is no more than one target in the scenario. To solve these challenges, we model the movement of the target by using a trajectory function of time (T-FoT). Data-driven T-FoT initiation and termination strategies are proposed for identifying the (re-)appearance and disappearance of the target. During the existence of the target, real target measurements are distinguished from clutter if the target indeed exists and is detected, in order to update the T-FoT at each scan for which we design a least-squares estimator. Simulations using either linear or nonlinear systems are conducted to demonstrate the effectiveness of our approach in comparison with the Bayes optimal Bernoulli filters. The results show that our approach is comparable to the perfectly-modeled filters, even outperforms them in some cases while requiring much less a-prior information and computing much faster.

Fast Marginalized Block Sparse Bayesian Learning Algorithm

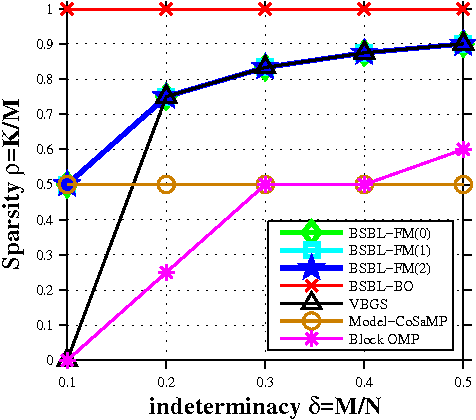
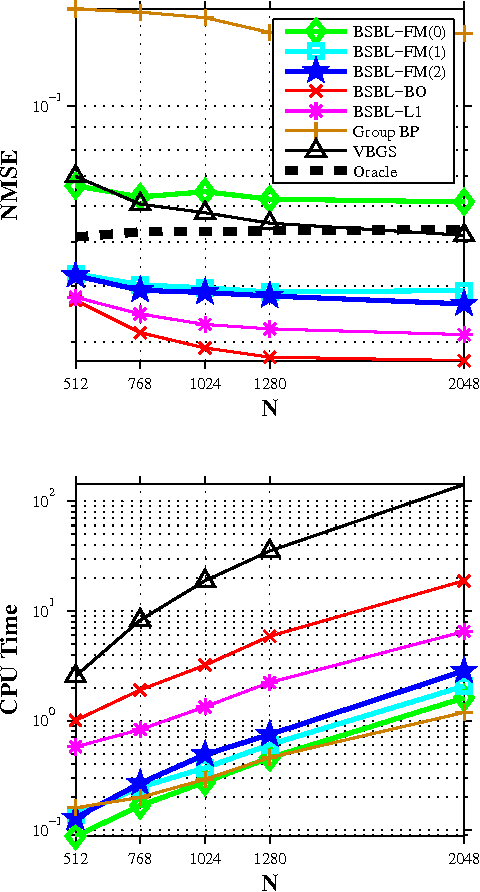
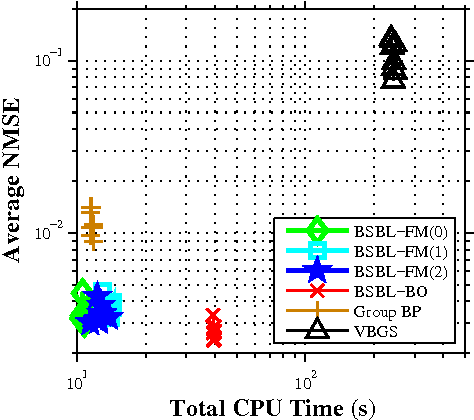
The performance of sparse signal recovery from noise corrupted, underdetermined measurements can be improved if both sparsity and correlation structure of signals are exploited. One typical correlation structure is the intra-block correlation in block sparse signals. To exploit this structure, a framework, called block sparse Bayesian learning (BSBL), has been proposed recently. Algorithms derived from this framework showed superior performance but they are not very fast, which limits their applications. This work derives an efficient algorithm from this framework, using a marginalized likelihood maximization method. Compared to existing BSBL algorithms, it has close recovery performance but is much faster. Therefore, it is more suitable for large scale datasets and applications requiring real-time implementation.

Scan-based Compressed Terahertz Imaging and Real-Time Reconstruction via the Complex-valued Fast Block Sparse Bayesian Learning Algorithm

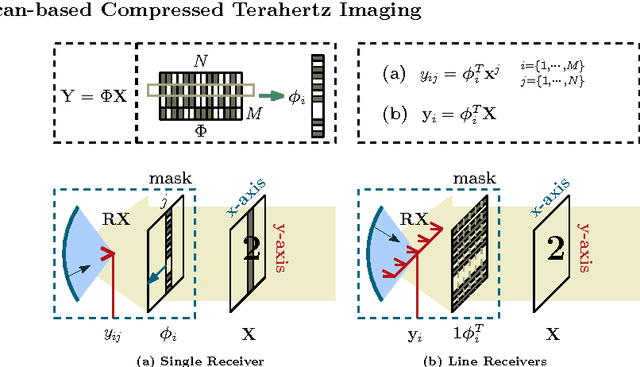
Compressed Sensing based Terahertz imaging (CS-THz) is a computational imaging technique. It uses only one THz receiver to accumulate the random modulated image measurements where the original THz image is reconstruct from these measurements using compressed sensing solvers. The advantage of the CS-THz is its reduced acquisition time compared with the raster scan mode. However, when it applied to large-scale two-dimensional (2D) imaging, the increased dimension resulted in both high computational complexity and excessive memory usage. In this paper, we introduced a novel CS-based THz imaging system that progressively compressed the THz image column by column. Therefore, the CS-THz system could be simplified with a much smaller sized modulator and reduced dimension. In order to utilize the block structure and the correlation of adjacent columns of the THz image, a complex-valued block sparse Bayesian learning algorithm was proposed. We conducted systematic evaluation of state-of-the-art CS algorithms under the scan based CS-THz architecture. The compression ratios and the choices of the sensing matrices were analyzed in detail using both synthetic and real-life THz images. Simulation results showed that both the scan based architecture and the proposed recovery algorithm were superior and efficient for large scale CS-THz applications.

The Annealing Sparse Bayesian Learning Algorithm

In this paper we propose a two-level hierarchical Bayesian model and an annealing schedule to re-enable the noise variance learning capability of the fast marginalized Sparse Bayesian Learning Algorithms. The performance such as NMSE and F-measure can be greatly improved due to the annealing technique. This algorithm tends to produce the most sparse solution under moderate SNR scenarios and can outperform most concurrent SBL algorithms while pertains small computational load.