Unsupervised feature selection via self-paced learning and low-redundant regularization

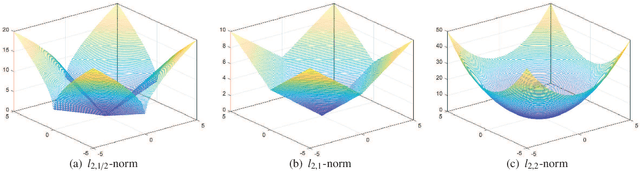
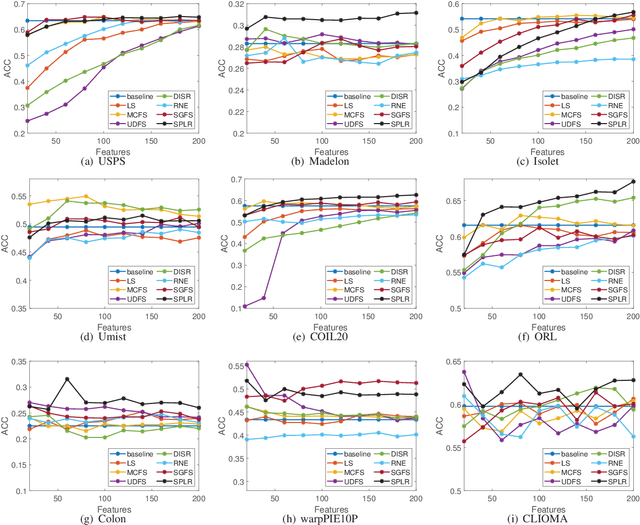
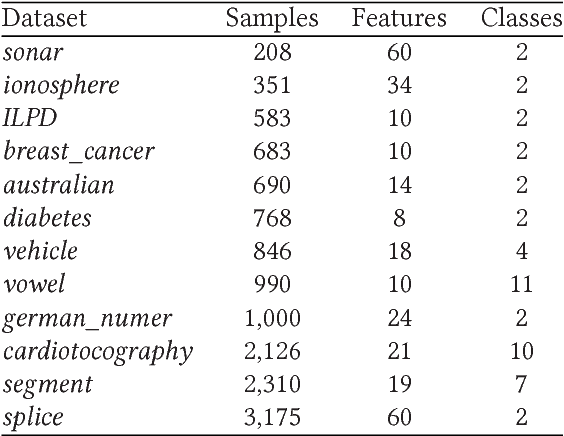
Much more attention has been paid to unsupervised feature selection nowadays due to the emergence of massive unlabeled data. The distribution of samples and the latent effect of training a learning method using samples in more effective order need to be considered so as to improve the robustness of the method. Self-paced learning is an effective method considering the training order of samples. In this study, an unsupervised feature selection is proposed by integrating the framework of self-paced learning and subspace learning. Moreover, the local manifold structure is preserved and the redundancy of features is constrained by two regularization terms. $L_{2,1/2}$-norm is applied to the projection matrix, which aims to retain discriminative features and further alleviate the effect of noise in the data. Then, an iterative method is presented to solve the optimization problem. The convergence of the method is proved theoretically and experimentally. The proposed method is compared with other state of the art algorithms on nine real-world datasets. The experimental results show that the proposed method can improve the performance of clustering methods and outperform other compared algorithms.

Reconstruction of Hidden Representation for Robust Feature Extraction

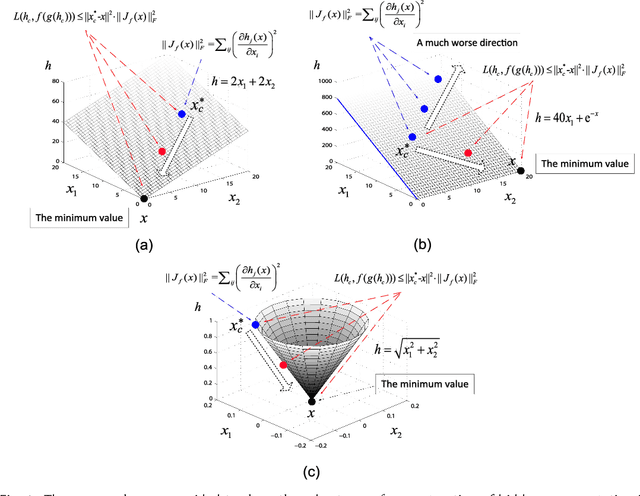
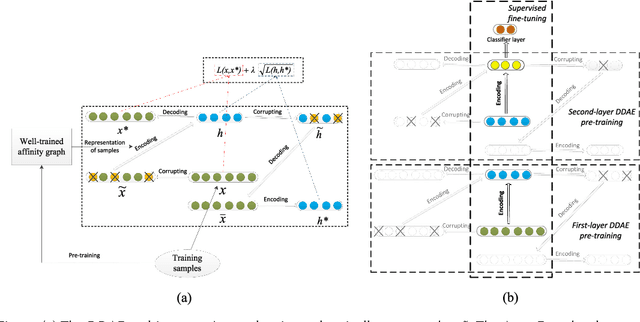
This paper aims to develop a new and robust approach to feature representation. Motivated by the success of Auto-Encoders, we first theoretical summarize the general properties of all algorithms that are based on traditional Auto-Encoders: 1) The reconstruction error of the input can not be lower than a lower bound, which can be viewed as a guiding principle for reconstructing the input. Additionally, when the input is corrupted with noises, the reconstruction error of the corrupted input also can not be lower than a lower bound. 2) The reconstruction of a hidden representation achieving its ideal situation is the necessary condition for the reconstruction of the input to reach the ideal state. 3) Minimizing the Frobenius norm of the Jacobian matrix of the hidden representation has a deficiency and may result in a much worse local optimum value. We believe that minimizing the reconstruction error of the hidden representation is more robust than minimizing the Frobenius norm of the Jacobian matrix of the hidden representation. Based on the above analysis, we propose a new model termed Double Denoising Auto-Encoders (DDAEs), which uses corruption and reconstruction on both the input and the hidden representation. We demonstrate that the proposed model is highly flexible and extensible and has a potentially better capability to learn invariant and robust feature representations. We also show that our model is more robust than Denoising Auto-Encoders (DAEs) for dealing with noises or inessential features. Furthermore, we detail how to train DDAEs with two different pre-training methods by optimizing the objective function in a combined and separate manner, respectively. Comparative experiments illustrate that the proposed model is significantly better for representation learning than the state-of-the-art models.