GBFRS: Robust Fuzzy Rough Sets via Granular-ball Computing

Fuzzy rough set theory is effective for processing datasets with complex attributes, supported by a solid mathematical foundation and closely linked to kernel methods in machine learning. Attribute reduction algorithms and classifiers based on fuzzy rough set theory exhibit promising performance in the analysis of high-dimensional multivariate complex data. However, most existing models operate at the finest granularity, rendering them inefficient and sensitive to noise, especially for high-dimensional big data. Thus, enhancing the robustness of fuzzy rough set models is crucial for effective feature selection. Muiti-garanularty granular-ball computing, a recent development, uses granular-balls of different sizes to adaptively represent and cover the sample space, performing learning based on these granular-balls. This paper proposes integrating multi-granularity granular-ball computing into fuzzy rough set theory, using granular-balls to replace sample points. The coarse-grained characteristics of granular-balls make the model more robust. Additionally, we propose a new method for generating granular-balls, scalable to the entire supervised method based on granular-ball computing. A forward search algorithm is used to select feature sequences by defining the correlation between features and categories through dependence functions. Experiments demonstrate the proposed model's effectiveness and superiority over baseline methods.

Unsupervised feature selection via self-paced learning and low-redundant regularization

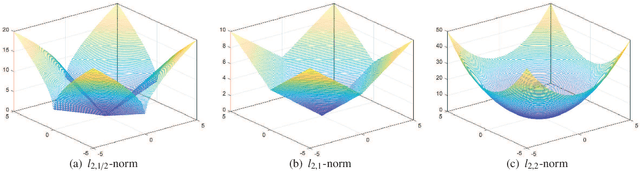
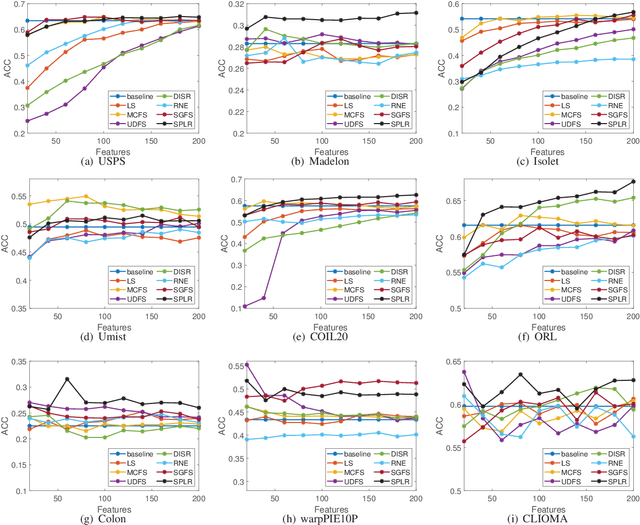
Much more attention has been paid to unsupervised feature selection nowadays due to the emergence of massive unlabeled data. The distribution of samples and the latent effect of training a learning method using samples in more effective order need to be considered so as to improve the robustness of the method. Self-paced learning is an effective method considering the training order of samples. In this study, an unsupervised feature selection is proposed by integrating the framework of self-paced learning and subspace learning. Moreover, the local manifold structure is preserved and the redundancy of features is constrained by two regularization terms. $L_{2,1/2}$-norm is applied to the projection matrix, which aims to retain discriminative features and further alleviate the effect of noise in the data. Then, an iterative method is presented to solve the optimization problem. The convergence of the method is proved theoretically and experimentally. The proposed method is compared with other state of the art algorithms on nine real-world datasets. The experimental results show that the proposed method can improve the performance of clustering methods and outperform other compared algorithms.