Unified Optimal Transport Framework for Universal Domain Adaptation

Universal Domain Adaptation (UniDA) aims to transfer knowledge from a source domain to a target domain without any constraints on label sets. Since both domains may hold private classes, identifying target common samples for domain alignment is an essential issue in UniDA. Most existing methods require manually specified or hand-tuned threshold values to detect common samples thus they are hard to extend to more realistic UniDA because of the diverse ratios of common classes. Moreover, they cannot recognize different categories among target-private samples as these private samples are treated as a whole. In this paper, we propose to use Optimal Transport (OT) to handle these issues under a unified framework, namely UniOT. First, an OT-based partial alignment with adaptive filling is designed to detect common classes without any predefined threshold values for realistic UniDA. It can automatically discover the intrinsic difference between common and private classes based on the statistical information of the assignment matrix obtained from OT. Second, we propose an OT-based target representation learning that encourages both global discrimination and local consistency of samples to avoid the over-reliance on the source. Notably, UniOT is the first method with the capability to automatically discover and recognize private categories in the target domain for UniDA. Accordingly, we introduce a new metric H^3-score to evaluate the performance in terms of both accuracy of common samples and clustering performance of private ones. Extensive experiments clearly demonstrate the advantages of UniOT over a wide range of state-of-the-art methods in UniDA.

Alternating Differentiation for Optimization Layers

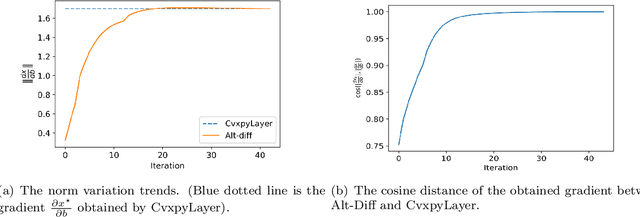
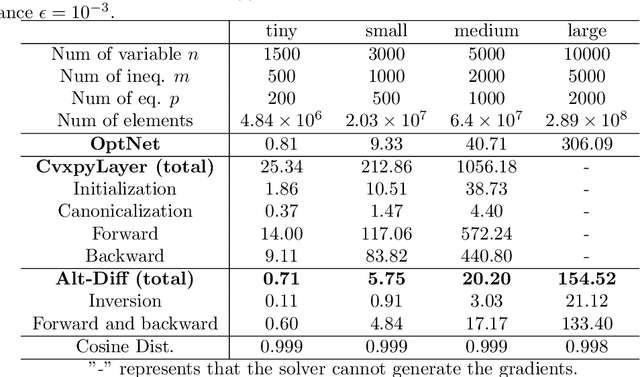
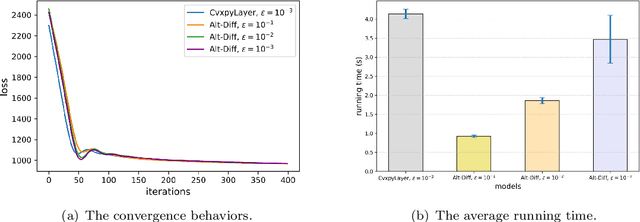
The idea of embedding optimization problems into deep neural networks as optimization layers to encode constraints and inductive priors has taken hold in recent years. Most existing methods focus on implicitly differentiating Karush-Kuhn-Tucker (KKT) conditions in a way that requires expensive computations on the Jacobian matrix, which can be slow and memory-intensive. In this paper, we developed a new framework, named Alternating Differentiation (Alt-Diff), that differentiates optimization problems (here, specifically in the form of convex optimization problems with polyhedral constraints) in a fast and recursive way. Alt-Diff decouples the differentiation procedure into a primal update and a dual update in an alternating way. Accordingly, Alt-Diff substantially decreases the dimensions of the Jacobian matrix and thus significantly increases the computational speed of implicit differentiation. Further, we present the computational complexity of the forward and backward pass of Alt-Diff and show that Alt-Diff enjoys quadratic computational complexity in the backward pass. Another notable difference between Alt-Diff and state-of-the-arts is that Alt-Diff can be truncated for the optimization layer. We theoretically show that: 1) Alt-Diff can converge to consistent gradients obtained by differentiating KKT conditions; 2) the error between the gradient obtained by the truncated Alt-Diff and by differentiating KKT conditions is upper bounded by the same order of variables' truncation error. Therefore, Alt-Diff can be truncated to further increases computational speed without sacrificing much accuracy. A series of comprehensive experiments demonstrate that Alt-Diff yields results comparable to the state-of-the-arts in far less time.