Interpretable Super-Resolution via a Learned Time-Series Representation

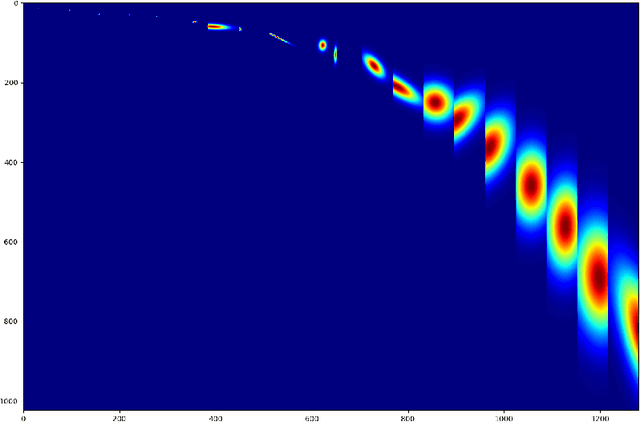
We develop an interpretable and learnable Wigner-Ville distribution that produces a super-resolved quadratic signal representation for time-series analysis. Our approach has two main hallmarks. First, it interpolates between known time-frequency representations (TFRs) in that it can reach super-resolution with increased time and frequency resolution beyond what the Heisenberg uncertainty principle prescribes and thus beyond commonly employed TFRs, Second, it is interpretable thanks to an explicit low-dimensional and physical parameterization of the Wigner-Ville distribution. We demonstrate that our approach is able to learn highly adapted TFRs and is ready and able to tackle various large-scale classification tasks, where we reach state-of-the-art performance compared to baseline and learned TFRs.

Semi-Supervised Learning Enabled by Multiscale Deep Neural Network Inversion

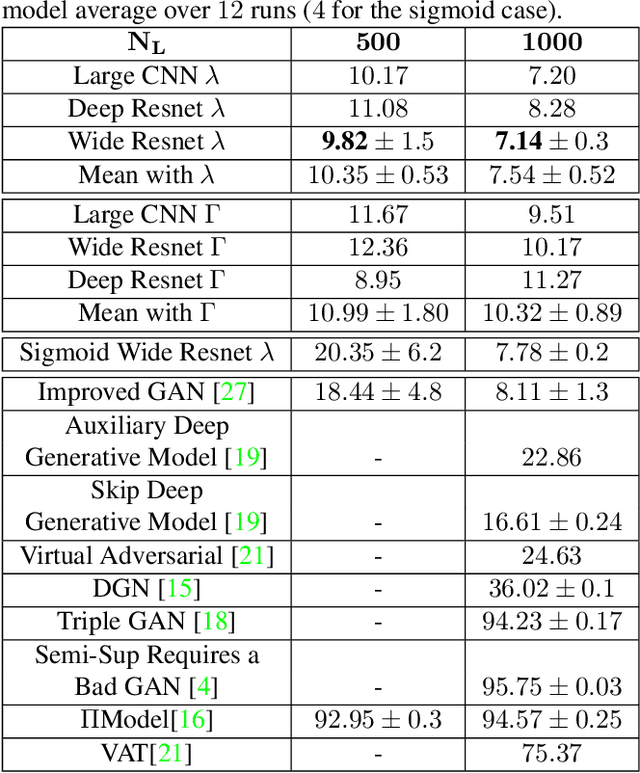
Deep Neural Networks (DNNs) provide state-of-the-art solutions in several difficult machine perceptual tasks. However, their performance relies on the availability of a large set of labeled training data, which limits the breadth of their applicability. Hence, there is a need for new {\em semi-supervised learning} methods for DNNs that can leverage both (a small amount of) labeled and unlabeled training data. In this paper, we develop a general loss function enabling DNNs of any topology to be trained in a semi-supervised manner without extra hyper-parameters. As opposed to current semi-supervised techniques based on topology-specific or unstable approaches, ours is both robust and general. We demonstrate that our approach reaches state-of-the-art performance on the SVHN ($9.82\%$ test error, with $500$ labels and wide Resnet) and CIFAR10 (16.38% test error, with 8000 labels and sigmoid convolutional neural network) data sets.

Linear Time Complexity Deep Fourier Scattering Network and Extension to Nonlinear Invariants

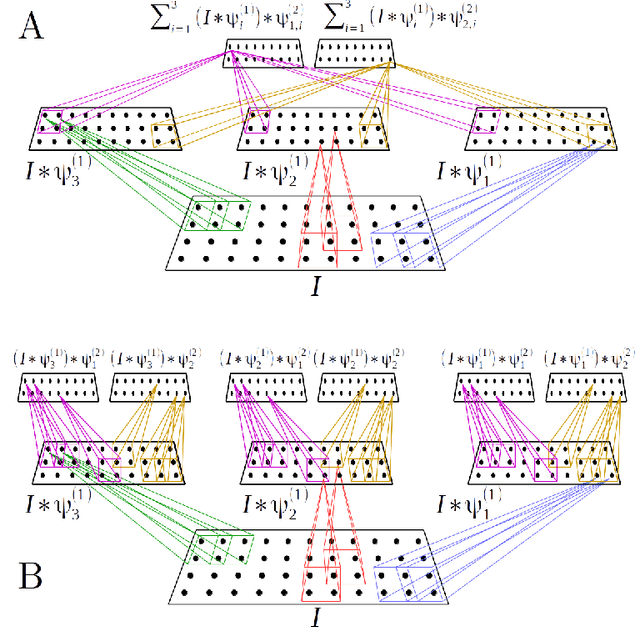
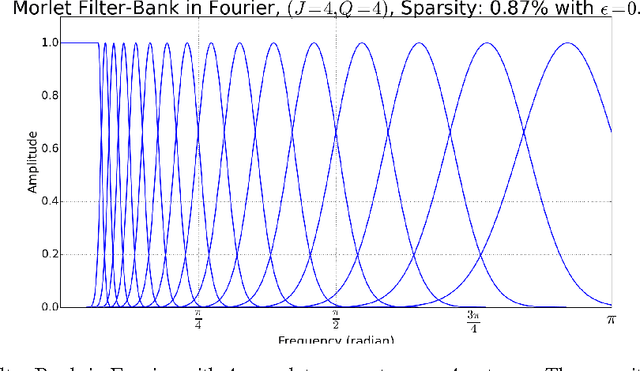
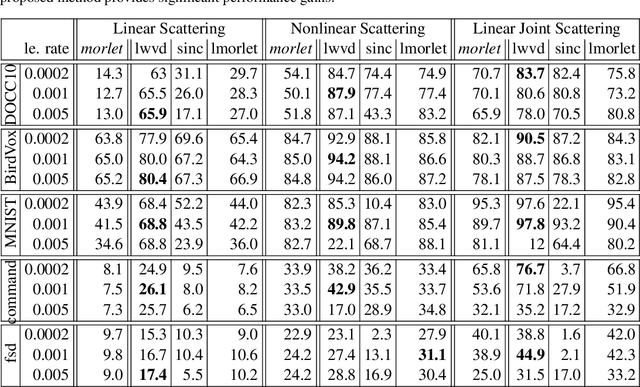
In this paper we propose a scalable version of a state-of-the-art deterministic time-invariant feature extraction approach based on consecutive changes of basis and nonlinearities, namely, the scattering network. The first focus of the paper is to extend the scattering network to allow the use of higher order nonlinearities as well as extracting nonlinear and Fourier based statistics leading to the required invariants of any inherently structured input. In order to reach fast convolutions and to leverage the intrinsic structure of wavelets, we derive our complete model in the Fourier domain. In addition of providing fast computations, we are now able to exploit sparse matrices due to extremely high sparsity well localized in the Fourier domain. As a result, we are able to reach a true linear time complexity with inputs in the Fourier domain allowing fast and energy efficient solutions to machine learning tasks. Validation of the features and computational results will be presented through the use of these invariant coefficients to perform classification on audio recordings of bird songs captured in multiple different soundscapes. In the end, the applicability of the presented solutions to deep artificial neural networks is discussed.

Sparse Penalty in Deep Belief Networks: Using the Mixed Norm Constraint

Deep Belief Networks (DBN) have been successfully applied on popular machine learning tasks. Specifically, when applied on hand-written digit recognition, DBNs have achieved approximate accuracy rates of 98.8%. In an effort to optimize the data representation achieved by the DBN and maximize their descriptive power, recent advances have focused on inducing sparse constraints at each layer of the DBN. In this paper we present a theoretical approach for sparse constraints in the DBN using the mixed norm for both non-overlapping and overlapping groups. We explore how these constraints affect the classification accuracy for digit recognition in three different datasets (MNIST, USPS, RIMES) and provide initial estimations of their usefulness by altering different parameters such as the group size and overlap percentage.