Analytical Probability Distributions and EM-Learning for Deep Generative Networks

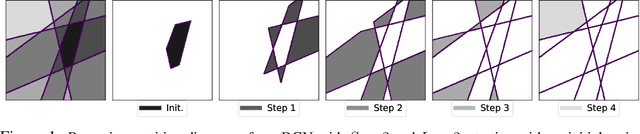
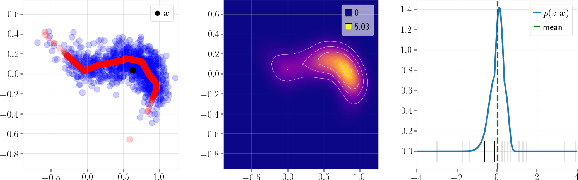
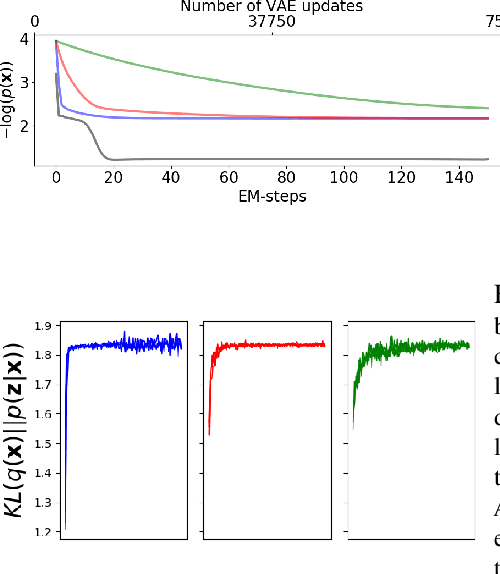
Deep Generative Networks (DGNs) with probabilistic modeling of their output and latent space are currently trained via Variational Autoencoders (VAEs). In the absence of a known analytical form for the posterior and likelihood expectation, VAEs resort to approximations, including (Amortized) Variational Inference (AVI) and Monte-Carlo (MC) sampling. We exploit the Continuous Piecewise Affine (CPA) property of modern DGNs to derive their posterior and marginal distributions as well as the latter's first moments. These findings enable us to derive an analytical Expectation-Maximization (EM) algorithm that enables gradient-free DGN learning. We demonstrate empirically that EM training of DGNs produces greater likelihood than VAE training. Our findings will guide the design of new VAE AVI that better approximate the true posterior and open avenues to apply standard statistical tools for model comparison, anomaly detection, and missing data imputation.

Max-Affine Spline Insights into Deep Generative Networks

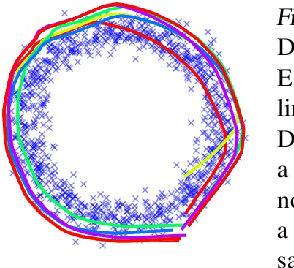
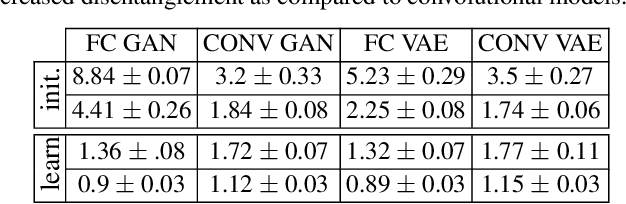
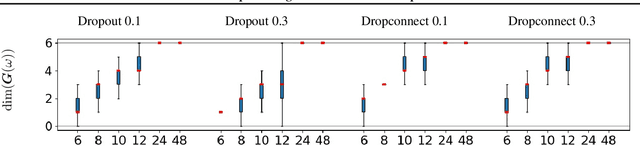
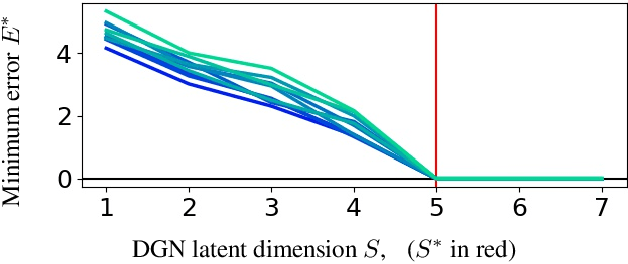
We connect a large class of Generative Deep Networks (GDNs) with spline operators in order to derive their properties, limitations, and new opportunities. By characterizing the latent space partition, dimension and angularity of the generated manifold, we relate the manifold dimension and approximation error to the sample size. The manifold-per-region affine subspace defines a local coordinate basis; we provide necessary and sufficient conditions relating those basis vectors with disentanglement. We also derive the output probability density mapped onto the generated manifold in terms of the latent space density, which enables the computation of key statistics such as its Shannon entropy. This finding also enables the computation of the GDN likelihood, which provides a new mechanism for model comparison as well as providing a quality measure for (generated) samples under the learned distribution. We demonstrate how low entropy and/or multimodal distributions are not naturally modeled by DGNs and are a cause of training instabilities.

Sparse Penalty in Deep Belief Networks: Using the Mixed Norm Constraint

Deep Belief Networks (DBN) have been successfully applied on popular machine learning tasks. Specifically, when applied on hand-written digit recognition, DBNs have achieved approximate accuracy rates of 98.8%. In an effort to optimize the data representation achieved by the DBN and maximize their descriptive power, recent advances have focused on inducing sparse constraints at each layer of the DBN. In this paper we present a theoretical approach for sparse constraints in the DBN using the mixed norm for both non-overlapping and overlapping groups. We explore how these constraints affect the classification accuracy for digit recognition in three different datasets (MNIST, USPS, RIMES) and provide initial estimations of their usefulness by altering different parameters such as the group size and overlap percentage.