Analytical Probability Distributions and EM-Learning for Deep Generative Networks
Paper and Code
Jun 17, 2020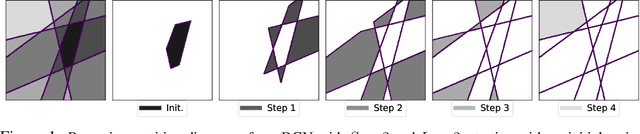

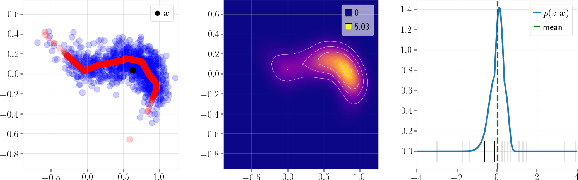
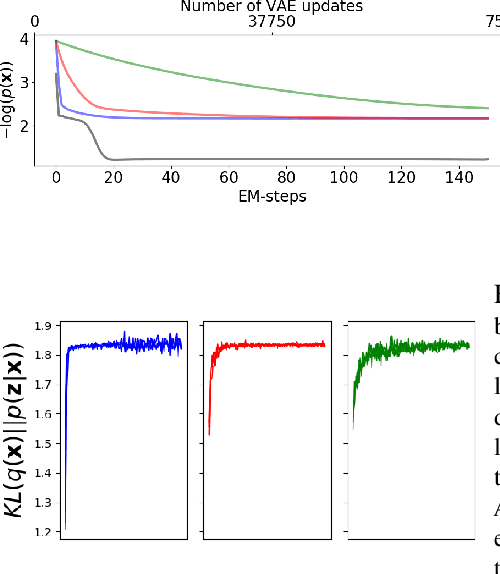
Deep Generative Networks (DGNs) with probabilistic modeling of their output and latent space are currently trained via Variational Autoencoders (VAEs). In the absence of a known analytical form for the posterior and likelihood expectation, VAEs resort to approximations, including (Amortized) Variational Inference (AVI) and Monte-Carlo (MC) sampling. We exploit the Continuous Piecewise Affine (CPA) property of modern DGNs to derive their posterior and marginal distributions as well as the latter's first moments. These findings enable us to derive an analytical Expectation-Maximization (EM) algorithm that enables gradient-free DGN learning. We demonstrate empirically that EM training of DGNs produces greater likelihood than VAE training. Our findings will guide the design of new VAE AVI that better approximate the true posterior and open avenues to apply standard statistical tools for model comparison, anomaly detection, and missing data imputation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge