Linear Time Complexity Deep Fourier Scattering Network and Extension to Nonlinear Invariants

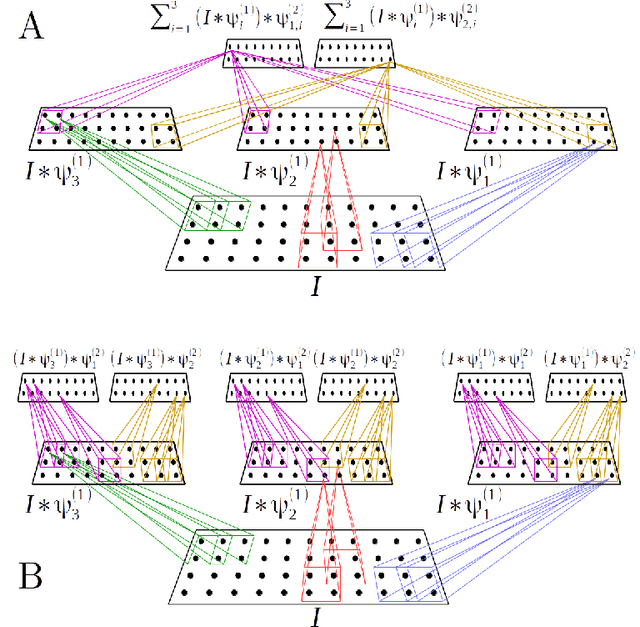
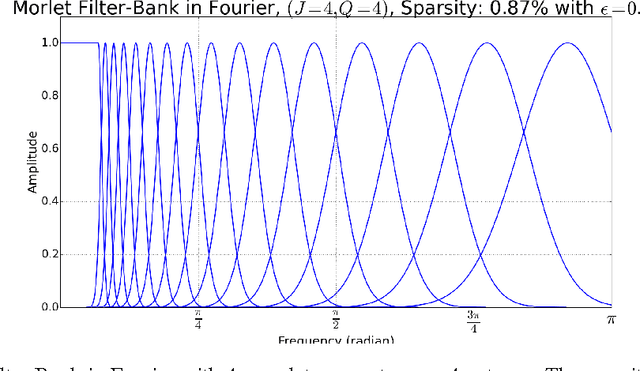
In this paper we propose a scalable version of a state-of-the-art deterministic time-invariant feature extraction approach based on consecutive changes of basis and nonlinearities, namely, the scattering network. The first focus of the paper is to extend the scattering network to allow the use of higher order nonlinearities as well as extracting nonlinear and Fourier based statistics leading to the required invariants of any inherently structured input. In order to reach fast convolutions and to leverage the intrinsic structure of wavelets, we derive our complete model in the Fourier domain. In addition of providing fast computations, we are now able to exploit sparse matrices due to extremely high sparsity well localized in the Fourier domain. As a result, we are able to reach a true linear time complexity with inputs in the Fourier domain allowing fast and energy efficient solutions to machine learning tasks. Validation of the features and computational results will be presented through the use of these invariant coefficients to perform classification on audio recordings of bird songs captured in multiple different soundscapes. In the end, the applicability of the presented solutions to deep artificial neural networks is discussed.