Henry Soldano
LIPN
Closed pattern mining of interval data and distributional data
Dec 09, 2022Abstract:We discuss pattern languages for closed pattern mining and learning of interval data and distributional data. We first introduce pattern languages relying on pairs of intersection-based constraints or pairs of inclusion based constraints, or both, applied to intervals. We discuss the encoding of such interval patterns as itemsets thus allowing to use closed itemsets mining and formal concept analysis programs. We experiment these languages on clustering and supervised learning tasks. Then we show how to extend the approach to address distributional data.
Exploring and mining attributed sequences of interactions
Jul 28, 2021
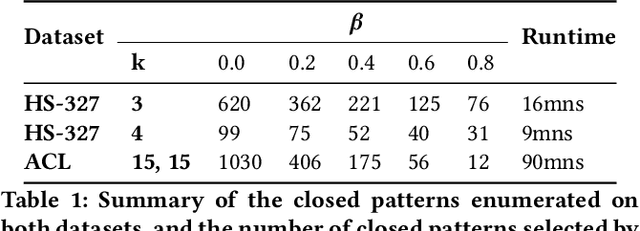
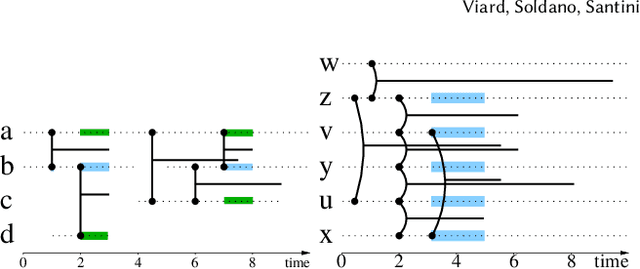
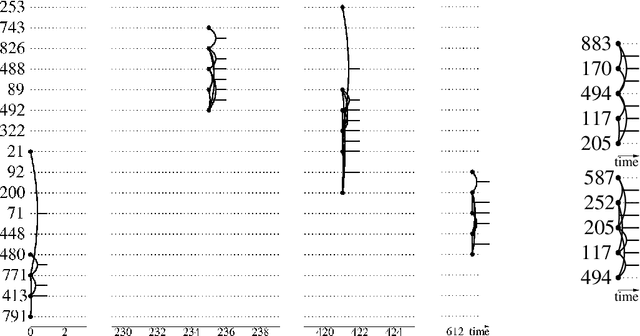
Abstract:We are faced with data comprised of entities interacting over time: this can be individuals meeting, customers buying products, machines exchanging packets on the IP network, among others. Capturing the dynamics as well as the structure of these interactions is of crucial importance for analysis. These interactions can almost always be labeled with content: group belonging, reviews of products, abstracts, etc. We model these stream of interactions as stream graphs, a recent framework to model interactions over time. Formal Concept Analysis provides a framework for analyzing concepts evolving within a context. Considering graphs as the context, it has recently been applied to perform closed pattern mining on social graphs. In this paper, we are interested in pattern mining in sequences of interactions. After recalling and extending notions from formal concept analysis on graphs to stream graphs, we introduce algorithms to enumerate closed patterns on a labeled stream graph, and introduce a way to select relevant closed patterns. We run experiments on two real-world datasets of interactions among students and citations between authors, and show both the feasibility and the relevance of our method.
Finite Confluences and Closed Pattern Mining
Feb 14, 2021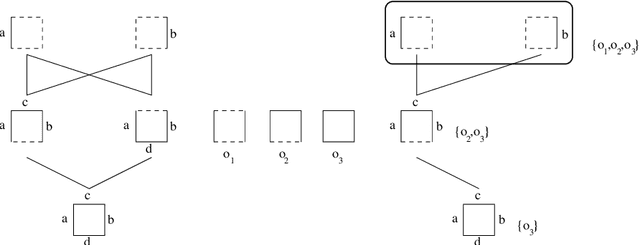
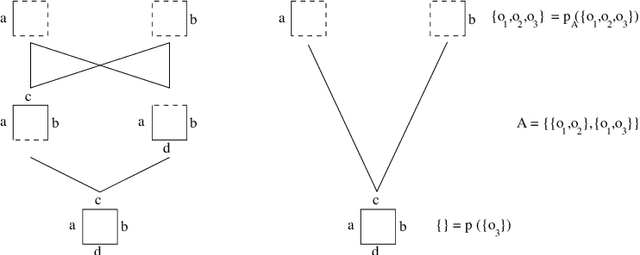
Abstract:The purpose of this article is to propose and investigate a partial order structure weaker than the lattice structure and which have nice properties regarding closure operators. We extend accordingly closed pattern mining and formal concept analysis to such structures we further call confluences. The primary motivation for investigating these structures is that it allows to reduce a lattice to a part whose elements are connected, as in some graph, still preserving a useful characterization of closure operators. Our investigation also considers how reducing one of the lattice involved in a Galois connection affects the structure of the closure operators ranges. When extending this way formal concept analysis we will focus on the intensional space, i.e. in reducing the pattern language, while recent investigations rather explored the reduction of the extensional space to connected elements.
Construction and Elicitation of a Black Box Model in the Game of Bridge
May 04, 2020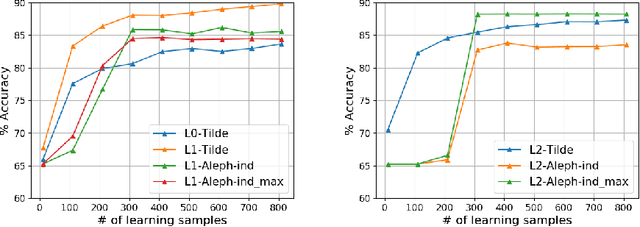
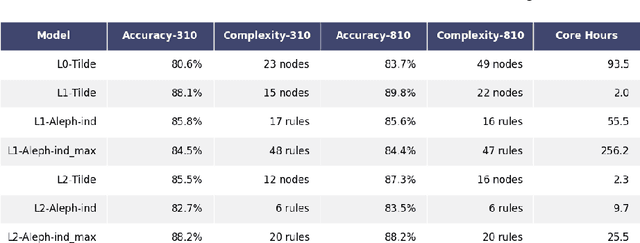
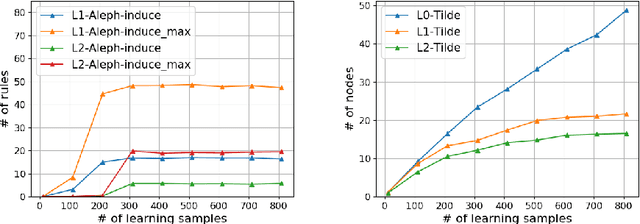

Abstract:We address the problem of building a decision model for a specific bidding situation in the game of Bridge. We propose the following multi-step methodology i) Build a set of examples for the decision problem and use simulations to associate a decision to each example ii) Use supervised relational learning to build an accurate and readable model iii) Perform a joint analysis between domain experts and data scientists to improve the learning language, including the production by experts of a handmade model iv) Build a better, more readable and accurate model.
Logical settings for concept learning from incomplete examples in First Order Logic
Jul 20, 2006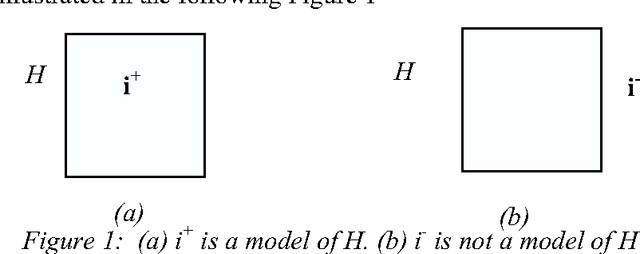
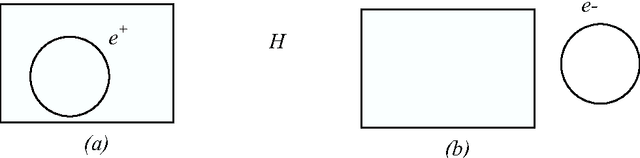
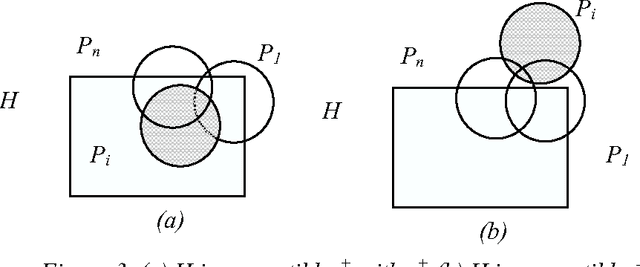
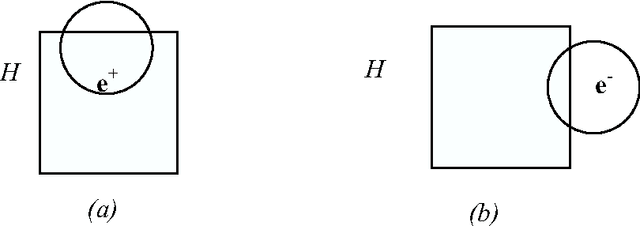
Abstract:We investigate here concept learning from incomplete examples. Our first purpose is to discuss to what extent logical learning settings have to be modified in order to cope with data incompleteness. More precisely we are interested in extending the learning from interpretations setting introduced by L. De Raedt that extends to relational representations the classical propositional (or attribute-value) concept learning from examples framework. We are inspired here by ideas presented by H. Hirsh in a work extending the Version space inductive paradigm to incomplete data. H. Hirsh proposes to slightly modify the notion of solution when dealing with incomplete examples: a solution has to be a hypothesis compatible with all pieces of information concerning the examples. We identify two main classes of incompleteness. First, uncertainty deals with our state of knowledge concerning an example. Second, generalization (or abstraction) deals with what part of the description of the example is sufficient for the learning purpose. These two main sources of incompleteness can be mixed up when only part of the useful information is known. We discuss a general learning setting, referred to as "learning from possibilities" that formalizes these ideas, then we present a more specific learning setting, referred to as "assumption-based learning" that cope with examples which uncertainty can be reduced when considering contextual information outside of the proper description of the examples. Assumption-based learning is illustrated on a recent work concerning the prediction of a consensus secondary structure common to a set of RNA sequences.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge