Finite Confluences and Closed Pattern Mining
Paper and Code
Feb 14, 2021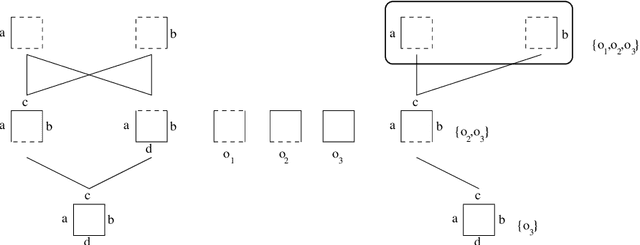
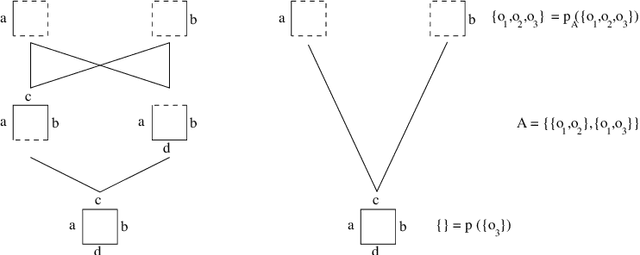
The purpose of this article is to propose and investigate a partial order structure weaker than the lattice structure and which have nice properties regarding closure operators. We extend accordingly closed pattern mining and formal concept analysis to such structures we further call confluences. The primary motivation for investigating these structures is that it allows to reduce a lattice to a part whose elements are connected, as in some graph, still preserving a useful characterization of closure operators. Our investigation also considers how reducing one of the lattice involved in a Galois connection affects the structure of the closure operators ranges. When extending this way formal concept analysis we will focus on the intensional space, i.e. in reducing the pattern language, while recent investigations rather explored the reduction of the extensional space to connected elements.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge