A weak convergence approach to large deviations for stochastic approximations

The theory of stochastic approximations form the theoretical foundation for studying convergence properties of many popular recursive learning algorithms in statistics, machine learning and statistical physics. Large deviations for stochastic approximations provide asymptotic estimates of the probability that the learning algorithm deviates from its expected path, given by a limit ODE, and the large deviation rate function gives insights to the most likely way that such deviations occur. In this paper we prove a large deviation principle for general stochastic approximations with state-dependent Markovian noise and decreasing step size. Using the weak convergence approach to large deviations, we generalize previous results for stochastic approximations and identify the appropriate scaling sequence for the large deviation principle. We also give a new representation for the rate function, in which the rate function is expressed as an action functional involving the family of Markov transition kernels. Examples of learning algorithms that are covered by the large deviation principle include stochastic gradient descent, persistent contrastive divergence and the Wang-Landau algorithm.

Marginal Thresholding in Noisy Image Segmentation

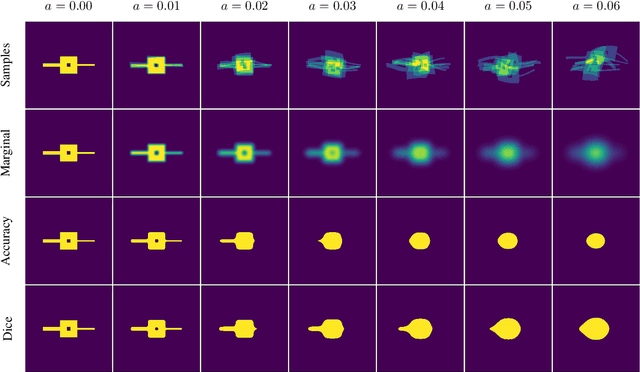
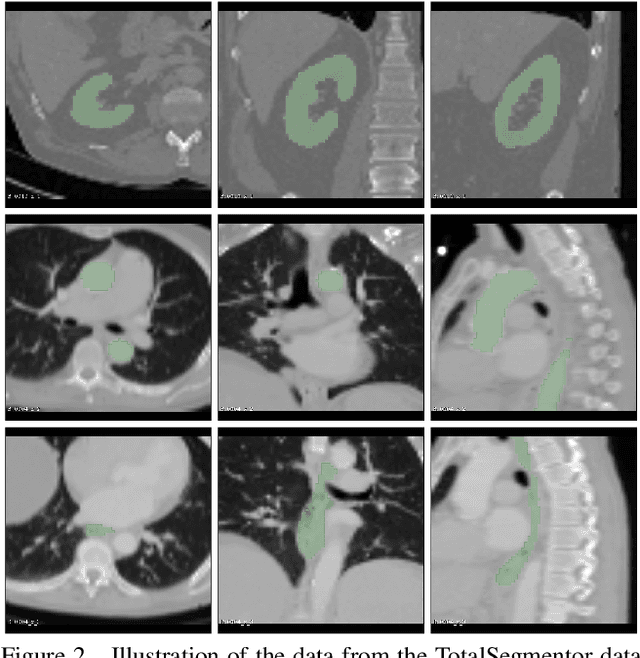
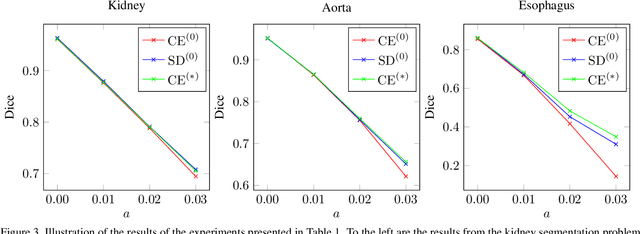
This work presents a study on label noise in medical image segmentation by considering a noise model based on Gaussian field deformations. Such noise is of interest because it yields realistic looking segmentations and because it is unbiased in the sense that the expected deformation is the identity mapping. Efficient methods for sampling and closed form solutions for the marginal probabilities are provided. Moreover, theoretically optimal solutions to the loss functions cross-entropy and soft-Dice are studied and it is shown how they diverge as the level of noise increases. Based on recent work on loss function characterization, it is shown that optimal solutions to soft-Dice can be recovered by thresholding solutions to cross-entropy with a particular a priori unknown threshold that efficiently can be computed. This raises the question whether the decrease in performance seen when using cross-entropy as compared to soft-Dice is caused by using the wrong threshold. The hypothesis is validated in 5-fold studies on three organ segmentation problems from the TotalSegmentor data set, using 4 different strengths of noise. The results show that changing the threshold leads the performance of cross-entropy to go from systematically worse than soft-Dice to similar or better results than soft-Dice.

Noisy Image Segmentation With Soft-Dice

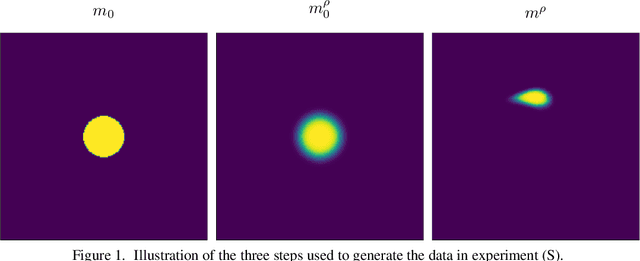
This paper presents a study on the soft-Dice loss, one of the most popular loss functions in medical image segmentation, for situations where noise is present in target labels. In particular, the set of optimal solutions are characterized and sharp bounds on the volume bias of these solutions are provided. It is further shown that a sequence of soft segmentations converging to optimal soft-Dice also converges to optimal Dice when converted to hard segmentations using thresholding. This is an important result because soft-Dice is often used as a proxy for maximizing the Dice metric. Finally, experiments confirming the theoretical results are provided.

On Image Segmentation With Noisy Labels: Characterization and Volume Properties of the Optimal Solutions to Accuracy and Dice

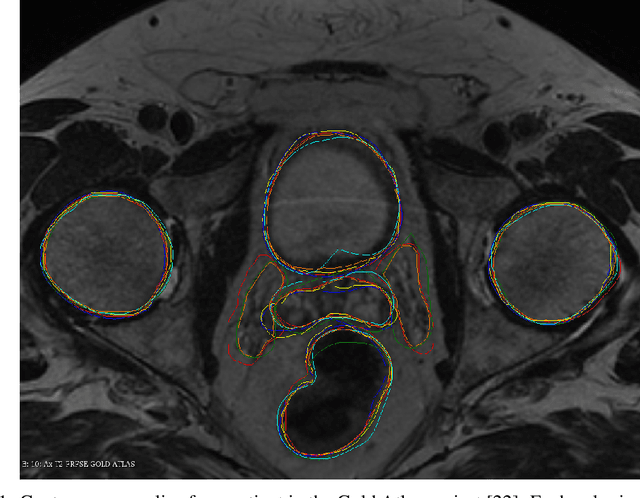
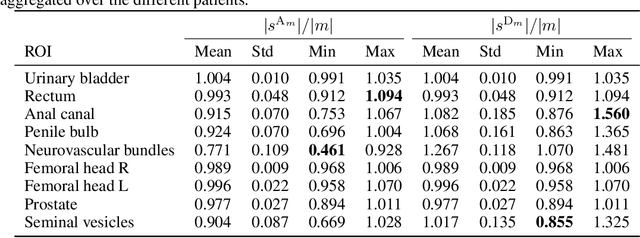
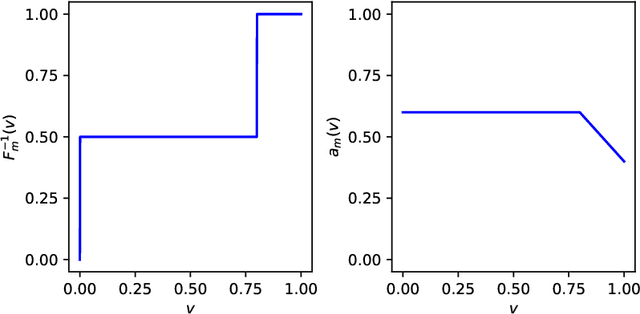
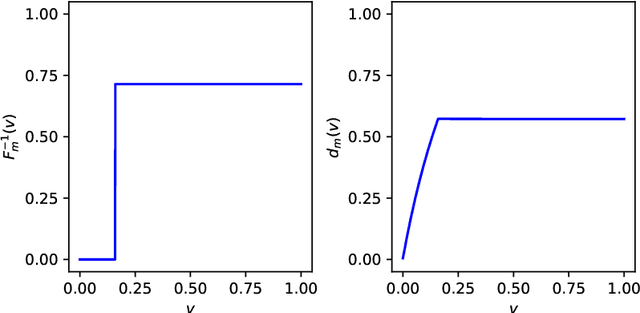
We study two of the most popular performance metrics in medical image segmentation, Accuracy and Dice, when the target labels are noisy. For both metrics, several statements related to characterization and volume properties of the set of optimal segmentations are proved, and associated experiments are provided. Our main insights are: (i) the volume of the solutions to both metrics may deviate significantly from the expected volume of the target, (ii) the volume of a solution to Accuracy is always less than or equal to the volume of a solution to Dice and (iii) the optimal solutions to both of these metrics coincide when the set of feasible segmentations is constrained to the set of segmentations with the volume equal to the expected volume of the target.

Variational Auto Encoder Gradient Clustering

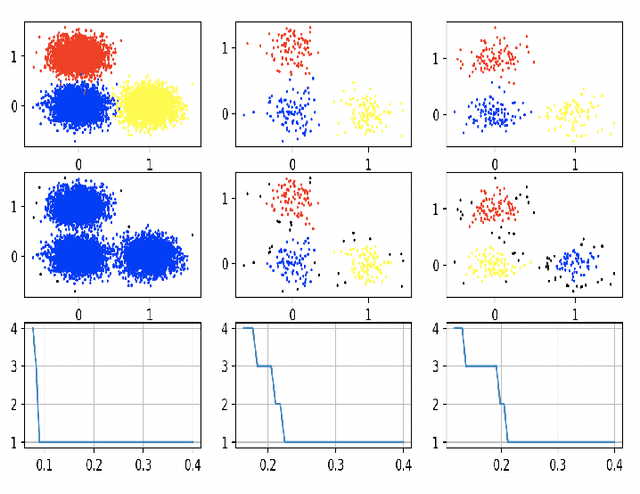
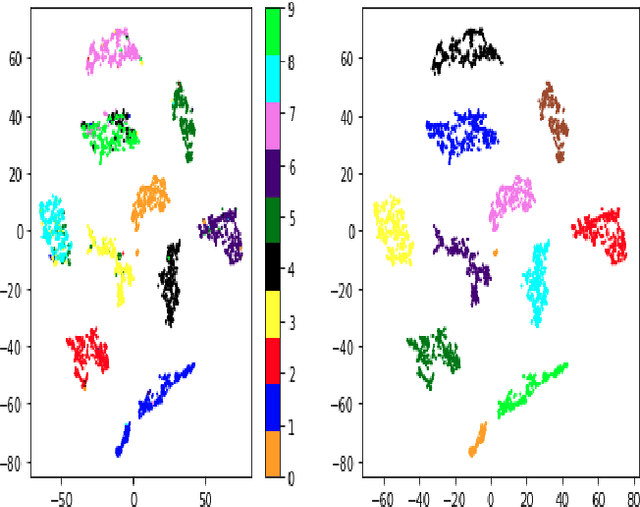
Clustering using deep neural network models have been extensively studied in recent years. Among the most popular frameworks are the VAE and GAN frameworks, which learns latent feature representations of data through encoder / decoder neural net structures. This is a suitable base for clustering tasks, as the latent space often seems to effectively capture the inherent essence of data, simplifying its manifold and reducing noise. In this article, the VAE framework is used to investigate how probability function gradient ascent over data points can be used to process data in order to achieve better clustering. Improvements in classification is observed comparing with unprocessed data, although state of the art results are not obtained. Processing data with gradient descent however results in more distinct cluster separation, making it simpler to investigate suitable hyper parameter settings such as the number of clusters. We propose a simple yet effective method for investigating suitable number of clusters for data, based on the DBSCAN clustering algorithm, and demonstrate that cluster number determination is facilitated with gradient processing. As an additional curiosity, we find that our baseline model used for comparison; a GMM on a t-SNE latent space for a VAE structure with weight one on reconstruction during training (autoencoder), yield state of the art results on the MNIST data, to our knowledge not beaten by any other existing model.

Particle Filter Bridge Interpolation

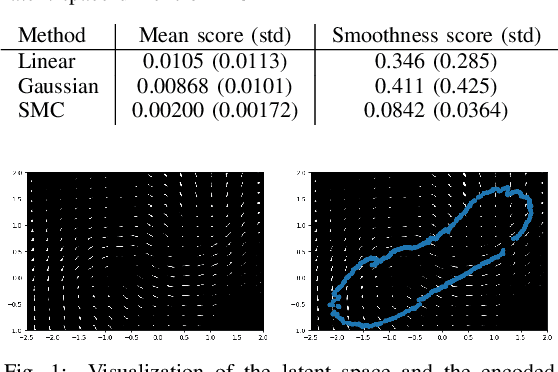
Auto encoding models have been extensively studied in recent years. They provide an efficient framework for sample generation, as well as for analysing feature learning. Furthermore, they are efficient in performing interpolations between data-points in semantically meaningful ways. In this paper, we build further on a previously introduced method for generating canonical, dimension independent, stochastic interpolations. Here, the distribution of interpolation paths is represented as the distribution of a bridge process constructed from an artificial random data generating process in the latent space, having the prior distribution as its invariant distribution. As a result the stochastic interpolation paths tend to reside in regions of the latent space where the prior has high mass. This is a desirable feature since, generally, such areas produce semantically meaningful samples. In this paper, we extend the bridge process method by introducing a discriminator network that accurately identifies areas of high latent representation density. The discriminator network is incorporated as a change of measure of the underlying bridge process and sampling of interpolation paths is implemented using sequential Monte Carlo. The resulting sampling procedure allows for greater variability in interpolation paths and stronger drift towards areas of high data density.