Noisy Image Segmentation With Soft-Dice

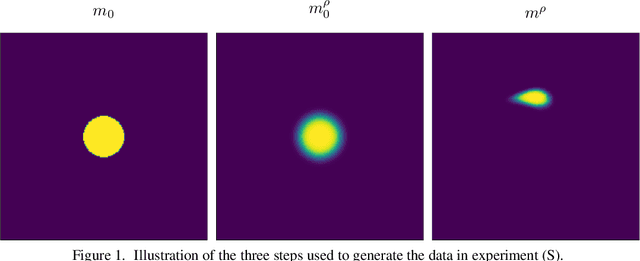
This paper presents a study on the soft-Dice loss, one of the most popular loss functions in medical image segmentation, for situations where noise is present in target labels. In particular, the set of optimal solutions are characterized and sharp bounds on the volume bias of these solutions are provided. It is further shown that a sequence of soft segmentations converging to optimal soft-Dice also converges to optimal Dice when converted to hard segmentations using thresholding. This is an important result because soft-Dice is often used as a proxy for maximizing the Dice metric. Finally, experiments confirming the theoretical results are provided.

On Image Segmentation With Noisy Labels: Characterization and Volume Properties of the Optimal Solutions to Accuracy and Dice

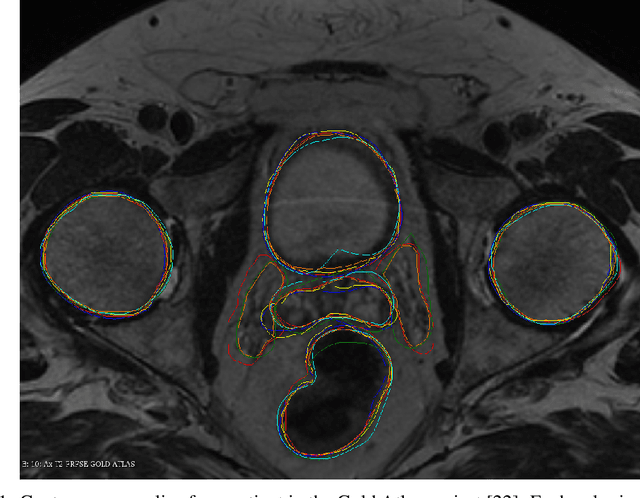
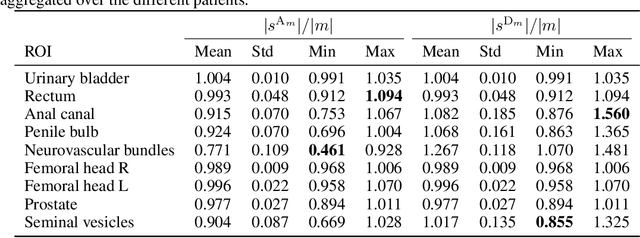
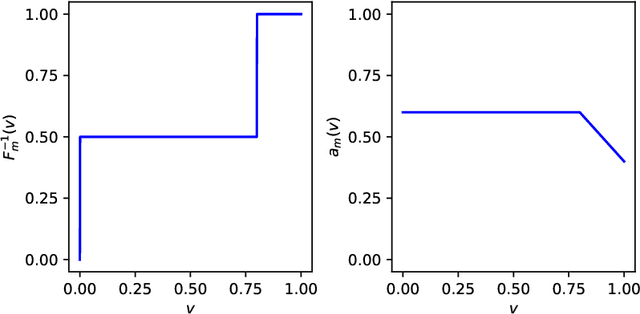
We study two of the most popular performance metrics in medical image segmentation, Accuracy and Dice, when the target labels are noisy. For both metrics, several statements related to characterization and volume properties of the set of optimal segmentations are proved, and associated experiments are provided. Our main insights are: (i) the volume of the solutions to both metrics may deviate significantly from the expected volume of the target, (ii) the volume of a solution to Accuracy is always less than or equal to the volume of a solution to Dice and (iii) the optimal solutions to both of these metrics coincide when the set of feasible segmentations is constrained to the set of segmentations with the volume equal to the expected volume of the target.