Variational Auto Encoder Gradient Clustering

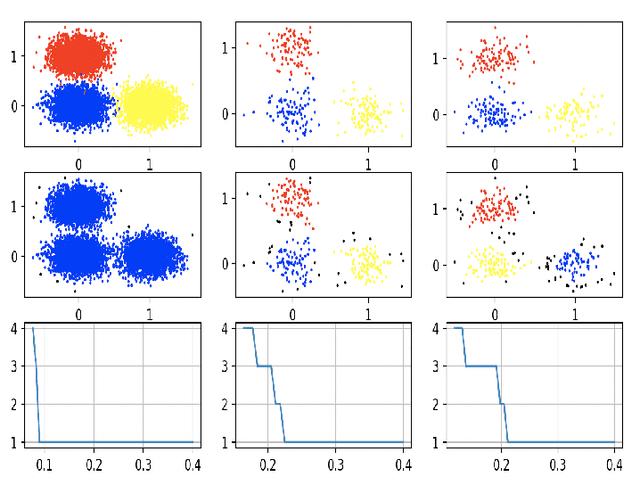
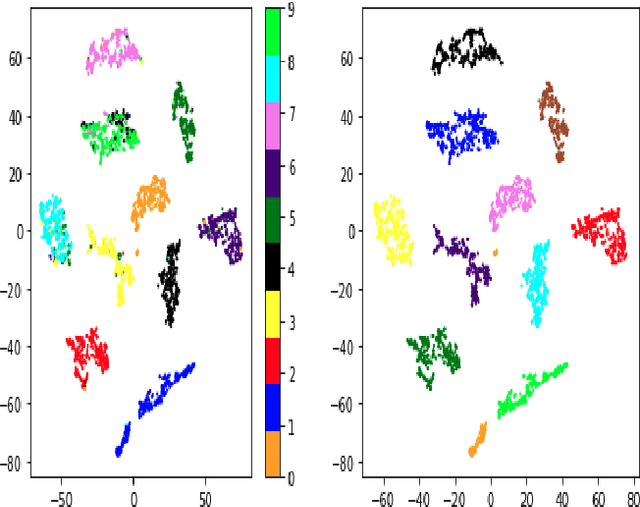
Clustering using deep neural network models have been extensively studied in recent years. Among the most popular frameworks are the VAE and GAN frameworks, which learns latent feature representations of data through encoder / decoder neural net structures. This is a suitable base for clustering tasks, as the latent space often seems to effectively capture the inherent essence of data, simplifying its manifold and reducing noise. In this article, the VAE framework is used to investigate how probability function gradient ascent over data points can be used to process data in order to achieve better clustering. Improvements in classification is observed comparing with unprocessed data, although state of the art results are not obtained. Processing data with gradient descent however results in more distinct cluster separation, making it simpler to investigate suitable hyper parameter settings such as the number of clusters. We propose a simple yet effective method for investigating suitable number of clusters for data, based on the DBSCAN clustering algorithm, and demonstrate that cluster number determination is facilitated with gradient processing. As an additional curiosity, we find that our baseline model used for comparison; a GMM on a t-SNE latent space for a VAE structure with weight one on reconstruction during training (autoencoder), yield state of the art results on the MNIST data, to our knowledge not beaten by any other existing model.

Particle Filter Bridge Interpolation

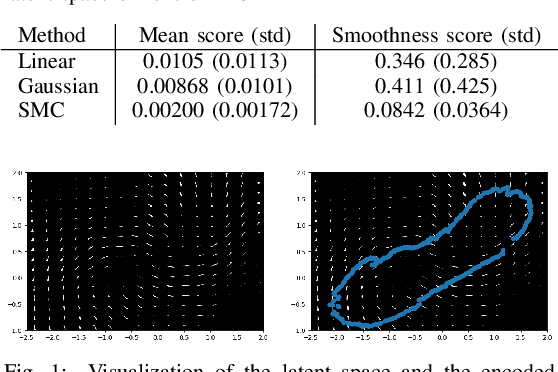
Auto encoding models have been extensively studied in recent years. They provide an efficient framework for sample generation, as well as for analysing feature learning. Furthermore, they are efficient in performing interpolations between data-points in semantically meaningful ways. In this paper, we build further on a previously introduced method for generating canonical, dimension independent, stochastic interpolations. Here, the distribution of interpolation paths is represented as the distribution of a bridge process constructed from an artificial random data generating process in the latent space, having the prior distribution as its invariant distribution. As a result the stochastic interpolation paths tend to reside in regions of the latent space where the prior has high mass. This is a desirable feature since, generally, such areas produce semantically meaningful samples. In this paper, we extend the bridge process method by introducing a discriminator network that accurately identifies areas of high latent representation density. The discriminator network is incorporated as a change of measure of the underlying bridge process and sampling of interpolation paths is implemented using sequential Monte Carlo. The resulting sampling procedure allows for greater variability in interpolation paths and stronger drift towards areas of high data density.