Mixed Matrix Completion in Complex Survey Sampling under Heterogeneous Missingness

Modern surveys with large sample sizes and growing mixed-type questionnaires require robust and scalable analysis methods. In this work, we consider recovering a mixed dataframe matrix, obtained by complex survey sampling, with entries following different canonical exponential distributions and subject to heterogeneous missingness. To tackle this challenging task, we propose a two-stage procedure: in the first stage, we model the entry-wise missing mechanism by logistic regression, and in the second stage, we complete the target parameter matrix by maximizing a weighted log-likelihood with a low-rank constraint. We propose a fast and scalable estimation algorithm that achieves sublinear convergence, and the upper bound for the estimation error of the proposed method is rigorously derived. Experimental results support our theoretical claims, and the proposed estimator shows its merits compared to other existing methods. The proposed method is applied to analyze the National Health and Nutrition Examination Survey data.

Transductive Matrix Completion with Calibration for Multi-Task Learning

Multi-task learning has attracted much attention due to growing multi-purpose research with multiple related data sources. Moreover, transduction with matrix completion is a useful method in multi-label learning. In this paper, we propose a transductive matrix completion algorithm that incorporates a calibration constraint for the features under the multi-task learning framework. The proposed algorithm recovers the incomplete feature matrix and target matrix simultaneously. Fortunately, the calibration information improves the completion results. In particular, we provide a statistical guarantee for the proposed algorithm, and the theoretical improvement induced by calibration information is also studied. Moreover, the proposed algorithm enjoys a sub-linear convergence rate. Several synthetic data experiments are conducted, which show the proposed algorithm out-performs other existing methods, especially when the target matrix is associated with the feature matrix in a nonlinear way.

Statistical inference using Regularized M-estimation in the reproducing kernel Hilbert space for handling missing data

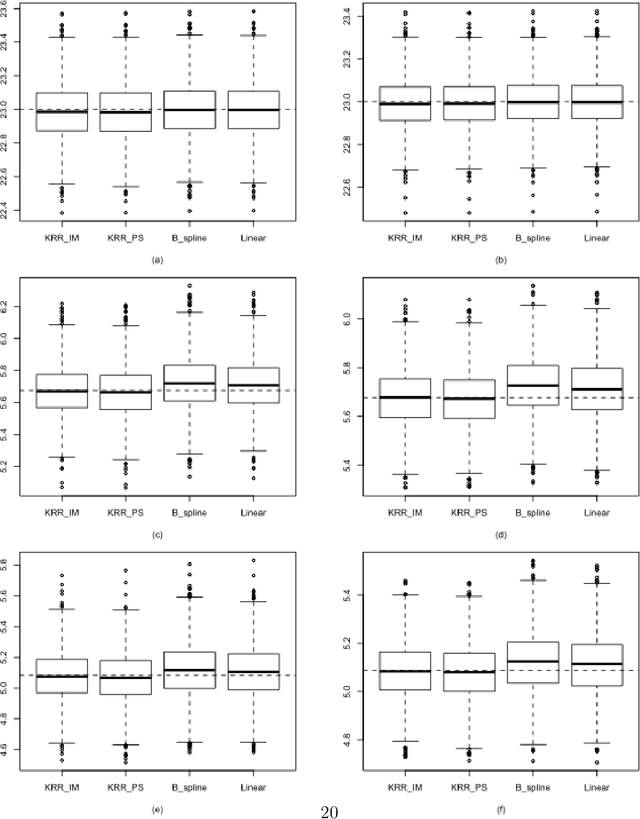
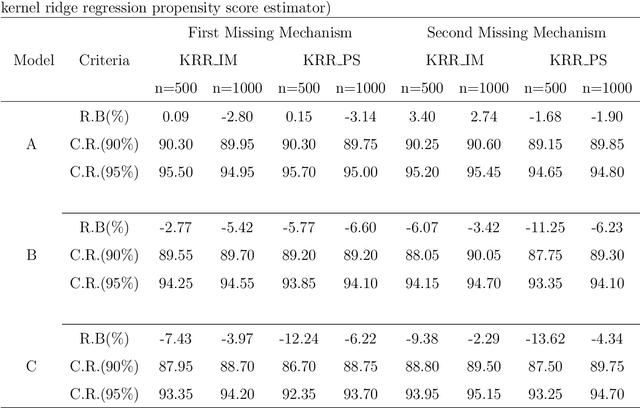
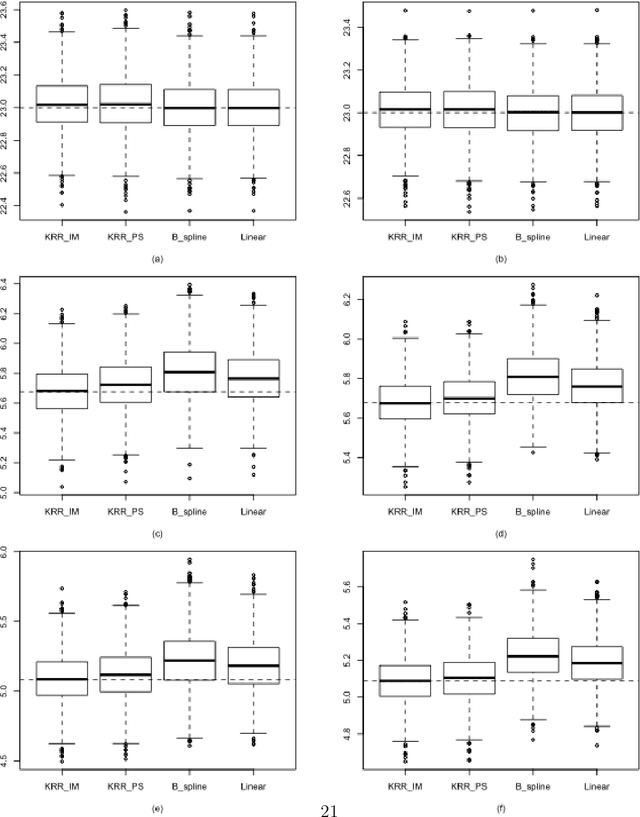
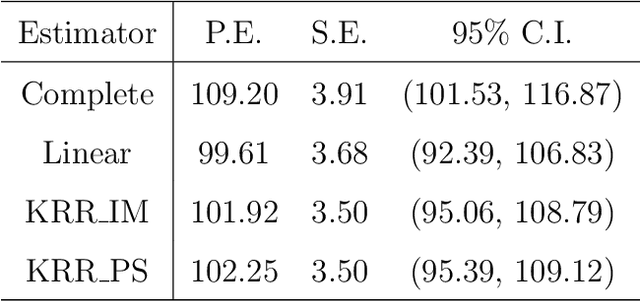
Imputation and propensity score weighting are two popular techniques for handling missing data. We address these problems using the regularized M-estimation techniques in the reproducing kernel Hilbert space. Specifically, we first use the kernel ridge regression to develop imputation for handling item nonresponse. While this nonparametric approach is potentially promising for imputation, its statistical properties are not investigated in the literature. Under some conditions on the order of the tuning parameter, we first establish the root-$n$ consistency of the kernel ridge regression imputation estimator and show that it achieves the lower bound of the semiparametric asymptotic variance. A nonparametric propensity score estimator using the reproducing kernel Hilbert space is also developed by a novel application of the maximum entropy method for the density ratio function estimation. We show that the resulting propensity score estimator is asymptotically equivalent to the kernel ridge regression imputation estimator. Results from a limited simulation study are also presented to confirm our theory. The proposed method is applied to analyze the air pollution data measured in Beijing, China.

Statistical Inference after Kernel Ridge Regression Imputation under item nonresponse

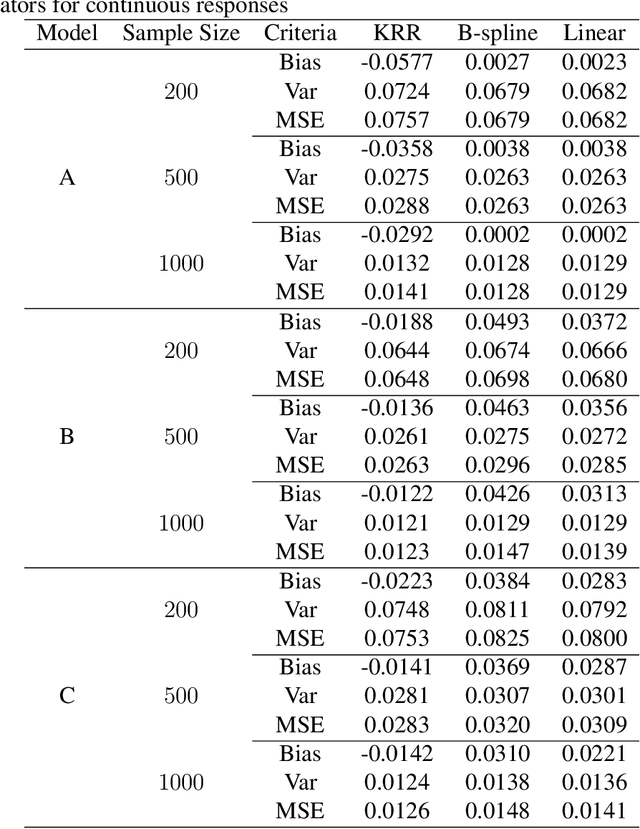
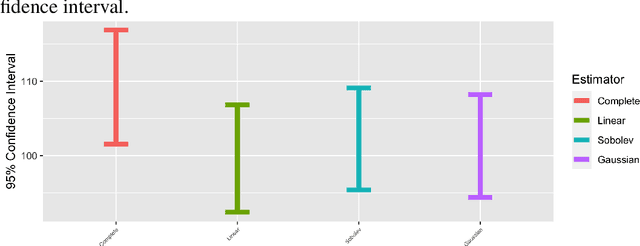
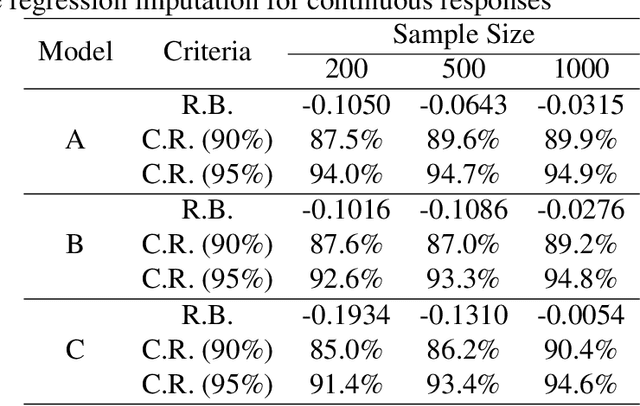
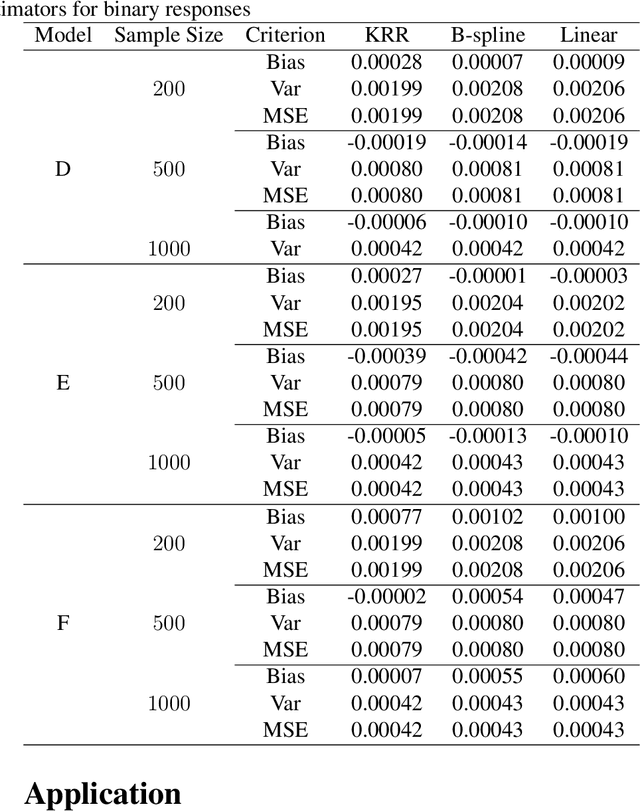
Imputation is a popular technique for handling missing data. We consider a nonparametric approach to imputation using the kernel ridge regression technique and propose consistent variance estimation. The proposed variance estimator is based on a linearization approach which employs the entropy method to estimate the density ratio. The root-n consistency of the imputation estimator is established when a Sobolev space is utilized in the kernel ridge regression imputation, which enables us to develop the proposed variance estimator. Synthetic data experiments are presented to confirm our theory.