LocalKMeans: Convergence of Lloyd's Algorithm with Distributed Local Iterations

In this paper, we analyze the classical $K$-means alternating-minimization algorithm, also known as Lloyd's algorithm (Lloyd, 1956), for a mixture of Gaussians in a data-distributed setting that incorporates local iteration steps. Assuming unlabeled data distributed across multiple machines, we propose an algorithm, LocalKMeans, that performs Lloyd's algorithm in parallel in the machines by running its iterations on local data, synchronizing only every $L$ of such local steps. We characterize the cost of these local iterations against the non-distributed setting, and show that the price paid for the local steps is a higher required signal-to-noise ratio. While local iterations were theoretically studied in the past for gradient-based learning methods, the analysis of unsupervised learning methods is more involved owing to the presence of latent variables, e.g. cluster identities, than that of an iterative gradient-based algorithm. To obtain our results, we adapt a virtual iterate method to work with a non-convex, non-smooth objective function, in conjunction with a tight statistical analysis of Lloyd steps.

Distributed Gradient Descent with Many Local Steps in Overparameterized Models

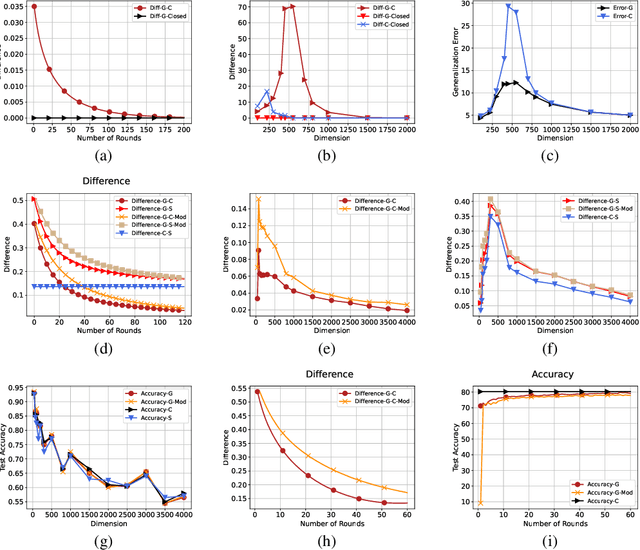
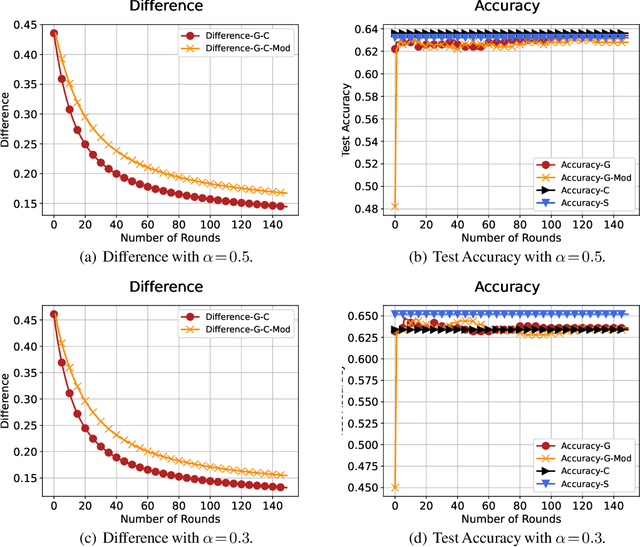
In distributed training of machine learning models, gradient descent with local iterative steps is a very popular method, variants of which are commonly known as Local-SGD or the Federated Averaging (FedAvg). In this method, gradient steps based on local datasets are taken independently in distributed compute nodes to update the local models, which are then aggregated intermittently. Although the existing convergence analysis suggests that with heterogeneous data, FedAvg encounters quick performance degradation as the number of local steps increases, it is shown to work quite well in practice, especially in the distributed training of large language models. In this work we try to explain this good performance from a viewpoint of implicit bias in Local Gradient Descent (Local-GD) with a large number of local steps. In overparameterized regime, the gradient descent at each compute node would lead the model to a specific direction locally. We characterize the dynamics of the aggregated global model and compare it to the centralized model trained with all of the data in one place. In particular, we analyze the implicit bias of gradient descent on linear models, for both regression and classification tasks. Our analysis shows that the aggregated global model converges exactly to the centralized model for regression tasks, and converges (in direction) to the same feasible set as centralized model for classification tasks. We further propose a Modified Local-GD with a refined aggregation and theoretically show it converges to the centralized model in direction for linear classification. We empirically verified our theoretical findings in linear models and also conducted experiments on distributed fine-tuning of pretrained neural networks to further apply our theory.

On the Tradeoff between Privacy Preservation and Byzantine-Robustness in Decentralized Learning

This paper jointly considers privacy preservation and Byzantine-robustness in decentralized learning. In a decentralized network, honest-but-curious agents faithfully follow the prescribed algorithm, but expect to infer their neighbors' private data from messages received during the learning process, while dishonest-and-Byzantine agents disobey the prescribed algorithm, and deliberately disseminate wrong messages to their neighbors so as to bias the learning process. For this novel setting, we investigate a generic privacy-preserving and Byzantine-robust decentralized stochastic gradient descent (SGD) framework, in which Gaussian noise is injected to preserve privacy and robust aggregation rules are adopted to counteract Byzantine attacks. We analyze its learning error and privacy guarantee, discovering an essential tradeoff between privacy preservation and Byzantine-robustness in decentralized learning -- the learning error caused by defending against Byzantine attacks is exacerbated by the Gaussian noise added to preserve privacy. Numerical experiments are conducted and corroborate our theoretical findings.

Optimal Compression of Unit Norm Vectors in the High Distortion Regime

Motivated by the need for communication-efficient distributed learning, we investigate the method for compressing a unit norm vector into the minimum number of bits, while still allowing for some acceptable level of distortion in recovery. This problem has been explored in the rate-distortion/covering code literature, but our focus is exclusively on the "high-distortion" regime. We approach this problem in a worst-case scenario, without any prior information on the vector, but allowing for the use of randomized compression maps. Our study considers both biased and unbiased compression methods and determines the optimal compression rates. It turns out that simple compression schemes are nearly optimal in this scenario. While the results are a mix of new and known, they are compiled in this paper for completeness.

Bridging Differential Privacy and Byzantine-Robustness via Model Aggregation

This paper aims at jointly addressing two seemly conflicting issues in federated learning: differential privacy (DP) and Byzantine-robustness, which are particularly challenging when the distributed data are non-i.i.d. (independent and identically distributed). The standard DP mechanisms add noise to the transmitted messages, and entangles with robust stochastic gradient aggregation to defend against Byzantine attacks. In this paper, we decouple the two issues via robust stochastic model aggregation, in the sense that our proposed DP mechanisms and the defense against Byzantine attacks have separated influence on the learning performance. Leveraging robust stochastic model aggregation, at each iteration, each worker calculates the difference between the local model and the global one, followed by sending the element-wise signs to the master node, which enables robustness to Byzantine attacks. Further, we design two DP mechanisms to perturb the uploaded signs for the purpose of privacy preservation, and prove that they are $(\epsilon,0)$-DP by exploiting the properties of noise distributions. With the tools of Moreau envelop and proximal point projection, we establish the convergence of the proposed algorithm when the cost function is nonconvex. We analyze the trade-off between privacy preservation and learning performance, and show that the influence of our proposed DP mechanisms is decoupled with that of robust stochastic model aggregation. Numerical experiments demonstrate the effectiveness of the proposed algorithm.

BROADCAST: Reducing Both Stochastic and Compression Noise to Robustify Communication-Efficient Federated Learning

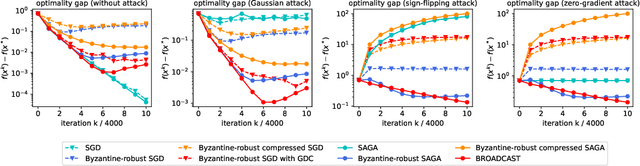
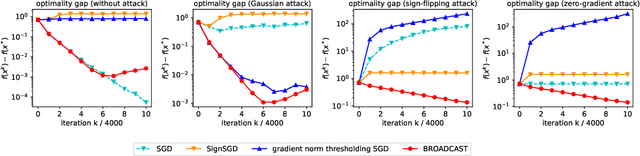
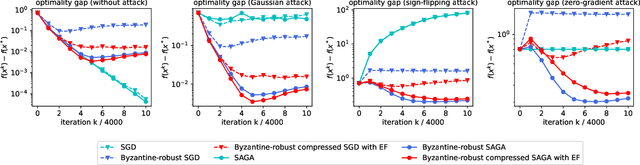
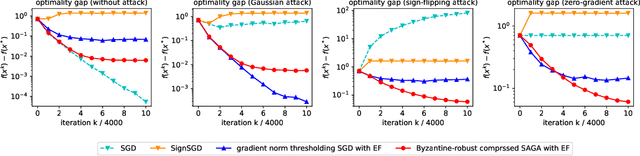
Communication between workers and the master node to collect local stochastic gradients is a key bottleneck in a large-scale federated learning system. Various recent works have proposed to compress the local stochastic gradients to mitigate the communication overhead. However, robustness to malicious attacks is rarely considered in such a setting. In this work, we investigate the problem of Byzantine-robust federated learning with compression, where the attacks from Byzantine workers can be arbitrarily malicious. We point out that a vanilla combination of compressed stochastic gradient descent (SGD) and geometric median-based robust aggregation suffers from both stochastic and compression noise in the presence of Byzantine attacks. In light of this observation, we propose to jointly reduce the stochastic and compression noise so as to improve the Byzantine-robustness. For the stochastic noise, we adopt the stochastic average gradient algorithm (SAGA) to gradually eliminate the inner variations of regular workers. For the compression noise, we apply the gradient difference compression and achieve compression for free. We theoretically prove that the proposed algorithm reaches a neighborhood of the optimal solution at a linear convergence rate, and the asymptotic learning error is in the same order as that of the state-of-the-art uncompressed method. Finally, numerical experiments demonstrate effectiveness of the proposed method.