Distributed Gradient Descent with Many Local Steps in Overparameterized Models
Paper and Code
Dec 10, 2024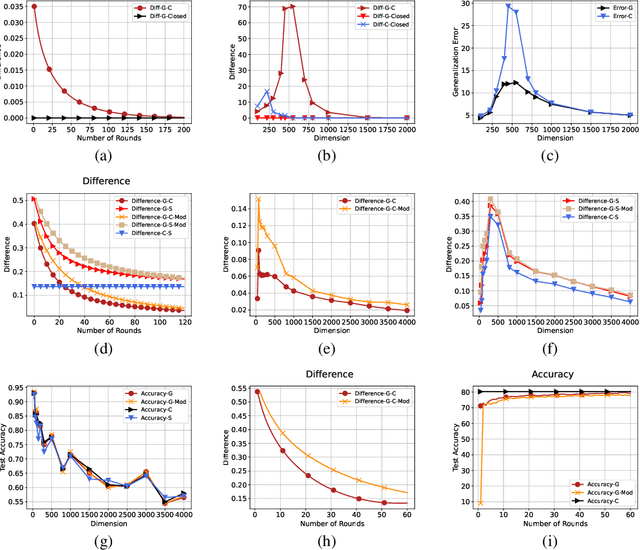
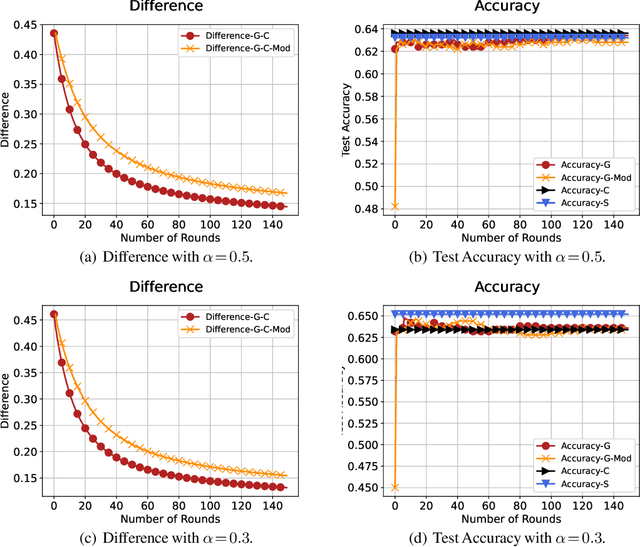
In distributed training of machine learning models, gradient descent with local iterative steps is a very popular method, variants of which are commonly known as Local-SGD or the Federated Averaging (FedAvg). In this method, gradient steps based on local datasets are taken independently in distributed compute nodes to update the local models, which are then aggregated intermittently. Although the existing convergence analysis suggests that with heterogeneous data, FedAvg encounters quick performance degradation as the number of local steps increases, it is shown to work quite well in practice, especially in the distributed training of large language models. In this work we try to explain this good performance from a viewpoint of implicit bias in Local Gradient Descent (Local-GD) with a large number of local steps. In overparameterized regime, the gradient descent at each compute node would lead the model to a specific direction locally. We characterize the dynamics of the aggregated global model and compare it to the centralized model trained with all of the data in one place. In particular, we analyze the implicit bias of gradient descent on linear models, for both regression and classification tasks. Our analysis shows that the aggregated global model converges exactly to the centralized model for regression tasks, and converges (in direction) to the same feasible set as centralized model for classification tasks. We further propose a Modified Local-GD with a refined aggregation and theoretically show it converges to the centralized model in direction for linear classification. We empirically verified our theoretical findings in linear models and also conducted experiments on distributed fine-tuning of pretrained neural networks to further apply our theory.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge