Towards Interpretable Deep Local Learning with Successive Gradient Reconciliation

Relieving the reliance of neural network training on a global back-propagation (BP) has emerged as a notable research topic due to the biological implausibility and huge memory consumption caused by BP. Among the existing solutions, local learning optimizes gradient-isolated modules of a neural network with local errors and has been proved to be effective even on large-scale datasets. However, the reconciliation among local errors has never been investigated. In this paper, we first theoretically study non-greedy layer-wise training and show that the convergence cannot be assured when the local gradient in a module w.r.t. its input is not reconciled with the local gradient in the previous module w.r.t. its output. Inspired by the theoretical result, we further propose a local training strategy that successively regularizes the gradient reconciliation between neighboring modules without breaking gradient isolation or introducing any learnable parameters. Our method can be integrated into both local-BP and BP-free settings. In experiments, we achieve significant performance improvements compared to previous methods. Particularly, our method for CNN and Transformer architectures on ImageNet is able to attain a competitive performance with global BP, saving more than 40% memory consumption.

On the Decision Boundaries of Deep Neural Networks: A Tropical Geometry Perspective

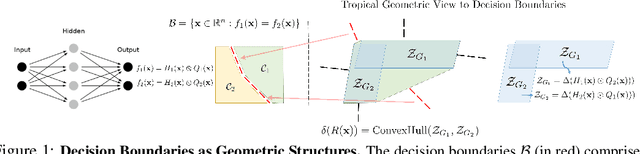
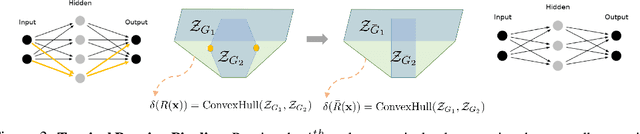
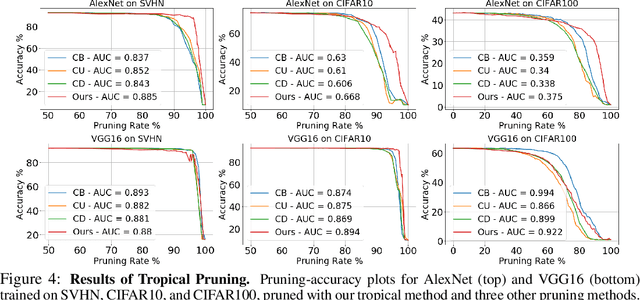
This work tackles the problem of characterizing and understanding the decision boundaries of neural networks with piecewise linear non-linearity activations. We use tropical geometry, a new development in the area of algebraic geometry, to characterize the decision boundaries of a simple neural network of the form (Affine, ReLU, Affine). Our main finding is that the decision boundaries are a subset of a tropical hypersurface, which is intimately related to a polytope formed by the convex hull of two zonotopes. The generators of these zonotopes are functions of the neural network parameters. This geometric characterization provides new perspective to three tasks. Specifically, we propose a new tropical perspective to the lottery ticket hypothesis, where we see the effect of different initializations on the tropical geometric representation of a network's decision boundaries. Moreover, we use this characterization to propose a new set of tropical regularizers, which directly deal with the decision boundaries of a network. We investigate the use of these regularizers in neural network pruning (by removing network parameters that do not contribute to the tropical geometric representation of the decision boundaries) and in generating adversarial input attacks (by producing input perturbations that explicitly perturb the decision boundaries' geometry and ultimately change the network's prediction).