VCG: A Multimodal Retrieval Framework for E-Commerce Video Feeds under Extreme Cold-Start Conditions

The digital commerce landscape is shifting from static, search-driven catalogs to dynamic, immersive video feeds. This transition introduces an ``extreme cold-start'' problem: unlike traditional items, new short-form videos lack the dense interaction history required for collaborative filtering. Furthermore, immersive feeds introduce strong position and duration biases that distort standard engagement signals. In this paper, we demonstrate the Video Candidate Generation (VCG) system, a scalable multimodal retrieval engine designed to solve these challenges in a large-scale e-commerce environment. By leveraging a domain-adapted vision-language model (based on CLIP), we map users and videos into a shared semantic space, enabling zero-shot retrieval based on visual content rather than behavioral history. We detail the system's architecture and present a rigorous evaluation comparing generative (LLM) vs. discriminative (CLIP) embeddings. Our results show that while generative models excel at attribute prediction, they suffer from embedding space collapse in retrieval tasks. Online A/B testing demonstrates that VCG effectively mitigates engagement biases, yielding a 50\% uplift in deep video completion. To showcase the system's capabilities, we present an interactive demonstration featuring three bi-directional retrieval scenarios: Product-to-Video, Video-to-Product, and Zero-Shot Semantic Search.

On the Decision Boundaries of Deep Neural Networks: A Tropical Geometry Perspective

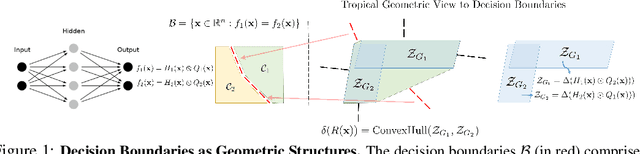
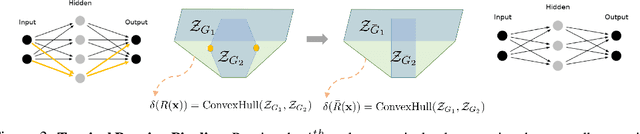
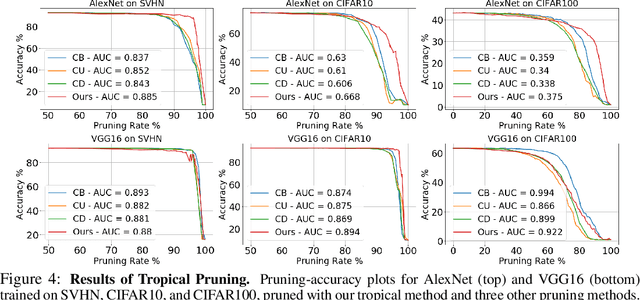
This work tackles the problem of characterizing and understanding the decision boundaries of neural networks with piecewise linear non-linearity activations. We use tropical geometry, a new development in the area of algebraic geometry, to characterize the decision boundaries of a simple neural network of the form (Affine, ReLU, Affine). Our main finding is that the decision boundaries are a subset of a tropical hypersurface, which is intimately related to a polytope formed by the convex hull of two zonotopes. The generators of these zonotopes are functions of the neural network parameters. This geometric characterization provides new perspective to three tasks. Specifically, we propose a new tropical perspective to the lottery ticket hypothesis, where we see the effect of different initializations on the tropical geometric representation of a network's decision boundaries. Moreover, we use this characterization to propose a new set of tropical regularizers, which directly deal with the decision boundaries of a network. We investigate the use of these regularizers in neural network pruning (by removing network parameters that do not contribute to the tropical geometric representation of the decision boundaries) and in generating adversarial input attacks (by producing input perturbations that explicitly perturb the decision boundaries' geometry and ultimately change the network's prediction).